题目内容
6.若把函数y=cosx-$\sqrt{3}$sinx的图象向右平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值为( )| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{6}$ |
分析 由条件利用三角函数的恒等变换化简函数的解析式,再利用函数y=Asin(ωx+φ)的图象变换规律,正弦函数、余弦函数的奇偶性,可得-m+$\frac{π}{3}$=kπ,k∈z,由此求得m的最小值.
解答 解:把函数y=cosx-$\sqrt{3}$sinx=2cos(x+$\frac{π}{3}$) 的图象向右平移m(m>0)个单位长度后,所得到的图象对应函数的解析式为y=2cos(x-m+$\frac{π}{3}$),
再根据所得图象关于y轴对称,可得y=2cos(x-m+$\frac{π}{3}$)为偶函数,
故有-m+$\frac{π}{3}$=kπ,k∈z,即 m=-kπ+$\frac{π}{3}$,则m的最小值为 $\frac{π}{3}$,
故选:A.
点评 本题主要考查三角函数的恒等变换,函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
16.如图是高中课程结构图:音乐所属课程是( )
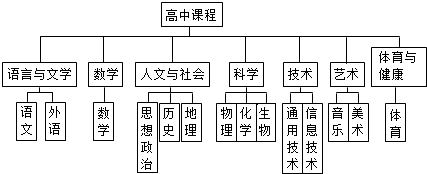

| A. | 艺术 | B. | 人文与社会 | C. | 技术 | D. | 科学 |
14.命题“所有实数的平方根都是正数”的否定为( )
| A. | 所有实数的平方都不是正数 | B. | 有的实数的平方是正数 | ||
| C. | 至少有一个实数的平方不是正数 | D. | 至少有一个实数的平方是正数 |
18.设x,y满足约束条件$\left\{\begin{array}{l}{x-y-3≤0}\\{x-2y≥0}\\{x+y-3≥0}\end{array}\right.$,则z=2x-y的最小值为( )
| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
15.设函数f(x)是定义在(-∞,+∞)上的增函数,实数a使得f(1-ax-x2)<f(2-a)对于任意x∈[0,1]都成立,则实数a的取值范围是( )
| A. | (-∞,1) | B. | [-2,0] | C. | (-2-2$\sqrt{2}$,-2+2$\sqrt{2}})$) | D. | [0,1] |
18.已知正方体的棱长为2$\sqrt{3}$,则外接球的体积为( )
| A. | 36π | B. | 288π | C. | 12π | D. | 18π |
 如图,点A是单位圆与x轴正半轴的交点,点B是单位圆上一个定点,点P是一个动点,且∠AOB=120°,∠AOP=θ(0<θ<π),$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$.
如图,点A是单位圆与x轴正半轴的交点,点B是单位圆上一个定点,点P是一个动点,且∠AOB=120°,∠AOP=θ(0<θ<π),$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$. 如图,在正三棱柱(底面是正三角形的直棱柱)ABC-A1B1C1中,D为AC的中点,
如图,在正三棱柱(底面是正三角形的直棱柱)ABC-A1B1C1中,D为AC的中点,