题目内容
10.已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的图象如图所示,则cosφ=-$\frac{1}{2}$.
分析 由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值,可得cosφ的值.
解答 解:由函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的图象,
可得$\frac{T}{2}$=$\frac{1}{2}$•$\frac{2π}{ω}$=$\frac{5π}{24}$-(-$\frac{π}{24}$),求得ω=4.
再根据五点法作图可得4×(-$\frac{π}{24}$)+φ=$\frac{π}{2}$,求得φ=$\frac{2π}{3}$,
故cosφ=cos$\frac{2π}{3}$=$-\frac{1}{2}$,
故答案为:-$\frac{1}{2}$.
点评 本题主要考查利用y=Asin(ωx+φ)的图象特征,由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值,属于基础题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
1.函数f(x)=21-x(x≥1)的值域为( )
| A. | [1,+∞) | B. | (-∞,1] | C. | (0,1] | D. | [0,1] |
18.设f(x)是定义在R上的奇函数,且在[0,+∞)上单调递增,则f(-3),f(-4)的大小关系是( )
| A. | f (-3)>f (-4) | B. | f (-3)<f (-4) | C. | f (-3)=f (-4) | D. | 无法比较 |
2.函数$f(x)=ln(x+2)-\frac{2}{x}$的零点所在的区间是( )
| A. | (3,4) | B. | (2,e) | C. | (0,1) | D. | (1,2) |
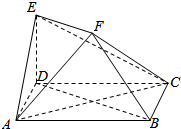 如图,ABCD是边长为2的正方形,ED⊥平面ABCD,ED=1,EF∥BD.
如图,ABCD是边长为2的正方形,ED⊥平面ABCD,ED=1,EF∥BD.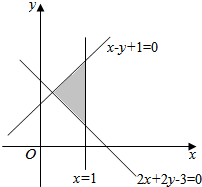 由x,y满足的约束条件,作出可行域如图中阴影部分(含边界)所示,则目标函数z=3x-y的最大值是$\frac{5}{2}$.
由x,y满足的约束条件,作出可行域如图中阴影部分(含边界)所示,则目标函数z=3x-y的最大值是$\frac{5}{2}$.