题目内容
已知椭圆C: 的四个顶点恰好是一边长为2,一内角为
的四个顶点恰好是一边长为2,一内角为 的菱形的四个顶点.
的菱形的四个顶点.
(I)求椭圆C的方程;
(II)若直线y =kx交椭圆C于A,B两点,在直线l:x+y-3=0上存在点P,使得 ΔPAB为等边三角形,求k的值.
(I) ; (II)
; (II) 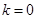 或
或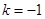 .
.
解析试题分析:(I)由图形的对称性及椭圆的几何性质,易得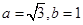 ,进而写出方程; (II) 先找到AB中垂线与l的交点,保证ΔPAB为等腰三角形,再满足
,进而写出方程; (II) 先找到AB中垂线与l的交点,保证ΔPAB为等腰三角形,再满足 即可保证ΔPAB为等边三角形,此外,注意对于特殊情形的讨论.
即可保证ΔPAB为等边三角形,此外,注意对于特殊情形的讨论.
试题解析:
(I)因为椭圆
 的四个顶点恰好是一边长为2,
的四个顶点恰好是一边长为2,
一内角为 的菱形的四个顶点,
的菱形的四个顶点,
所以 ,椭圆
,椭圆 的方程为
的方程为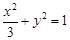 . 4分
. 4分
(II)设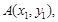 则
则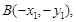
当直线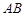 的斜率为
的斜率为 时,
时,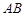 的垂直平分线就是
的垂直平分线就是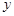 轴,
轴,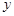 轴与直线
轴与直线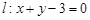 的交点为
的交点为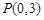 ,
,
又因为 ,所以
,所以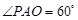 ,
,
所以 是等边三角形,所以
是等边三角形,所以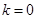 满足条件; 6分
满足条件; 6分
当直线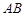 的斜率存在且不为
的斜率存在且不为 时,设
时,设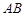 的方程为
的方程为
所以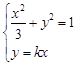 ,化简得
,化简得
所以 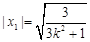 ,则
,则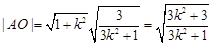 8分
8分
设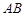 的垂直平分线为
的垂直平分线为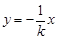 ,它与直线
,它与直线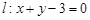 的交点记为
的交点记为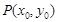
所以 ,解得
,解得 ,
,
则 10分
10分
因为 为等边三角形, 所以应有
为等边三角形, 所以应有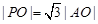
代入得到 ,解得
,解得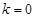 (舍),
(舍), 13分
13分
综上可知,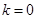 或
或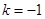 14分
14分
考点:直线与圆锥曲线的位置关系.

练习册系列答案
相关题目
已知椭圆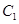 ,抛物线
,抛物线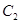 的焦点均在
的焦点均在 轴上,
轴上,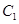 的中心和
的中心和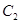 的顶点均为原点
的顶点均为原点 ,每条曲线上取两个点,将其坐标记录于表中:
,每条曲线上取两个点,将其坐标记录于表中:
 |  | 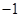 | 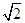 |  |
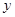 |  | 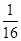 |  |  |
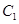 ,
,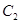 的标准方程;
的标准方程;(2)设斜率不为0的动直线
 与
与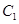 有且只有一个公共点
有且只有一个公共点 ,且与
,且与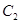 的准线交于
的准线交于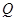 ,试探究:在坐标平面内是否存在定点
,试探究:在坐标平面内是否存在定点 ,使得以
,使得以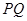 为直径的圆恒过点
为直径的圆恒过点 ?若存在,求出
?若存在,求出 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.  的长轴两端点分别为
的长轴两端点分别为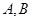 ,
, 是椭圆上的动点,以
是椭圆上的动点,以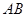 为一边在
为一边在 轴下方作矩形
轴下方作矩形 ,使
,使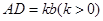 ,
,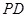 交
交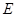 ,
, 交
交 .
.
 ,且
,且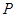 为椭圆上顶点时,
为椭圆上顶点时, 的面积为12,点
的面积为12,点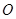 到直线
到直线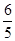 ,求椭圆的方程;
,求椭圆的方程;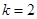 ,试证明:
,试证明: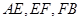 成等比数列.
成等比数列.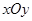 中,曲线
中,曲线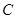 的参数方程为:
的参数方程为: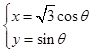 (
(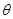 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系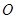 为极点,以
为极点,以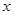 轴正半轴为极轴)中,直线
轴正半轴为极轴)中,直线 的极坐标方程为:
的极坐标方程为: .
.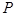 是曲线
是曲线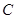 :
:
 ,称圆心在原点
,称圆心在原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 ,且其短轴上的一个端点到
,且其短轴上的一个端点到 的距离为
的距离为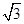 .
.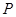 是椭圆
是椭圆 ,使得
,使得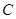 :
: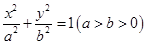 的离心率为
的离心率为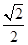 ,左焦点为
,左焦点为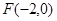 .
. 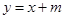 与曲线
与曲线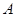 、
、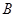 两点,且线段
两点,且线段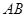 的中点
的中点 在圆
在圆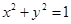 上,求
上,求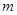 的值.
的值. 、
、 是椭圆
是椭圆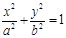
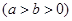 的左、右焦点,且离心率
的左、右焦点,且离心率 ,点
,点 为椭圆上的一个动点,
为椭圆上的一个动点,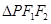 的内切圆面积的最大值为
的内切圆面积的最大值为 .
. 是椭圆上不重合的四个点,满足向量
是椭圆上不重合的四个点,满足向量 与
与 共线,
共线,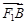 与
与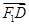 共
共 ,求
,求 的取值范围.
的取值范围.  有相同的焦点,与双曲线
有相同的焦点,与双曲线 有相同渐近线,求双曲线方程.
有相同渐近线,求双曲线方程.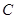 的顶点为原点,其焦点
的顶点为原点,其焦点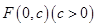 到直线
到直线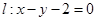 的距离为
的距离为 .设
.设 为直线
为直线 上的点,过点
上的点,过点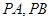 ,其中
,其中 为切点.
为切点. 为直线
为直线 的方程;
的方程; 的最小值.
的最小值.