题目内容
已知椭圆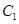 ,抛物线
,抛物线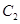 的焦点均在
的焦点均在 轴上,
轴上,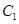 的中心和
的中心和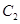 的顶点均为原点
的顶点均为原点 ,每条曲线上取两个点,将其坐标记录于表中:
,每条曲线上取两个点,将其坐标记录于表中:
 |  | 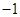 | 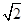 | 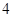 |
 | 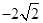 | 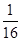 | 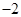 | 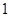 |
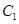 ,
,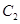 的标准方程;
的标准方程;(2)设斜率不为0的动直线
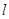 与
与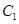 有且只有一个公共点
有且只有一个公共点 ,且与
,且与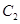 的准线交于
的准线交于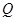 ,试探究:在坐标平面内是否存在定点
,试探究:在坐标平面内是否存在定点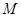 ,使得以
,使得以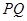 为直径的圆恒过点
为直径的圆恒过点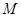 ?若存在,求出
?若存在,求出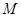 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
(1) 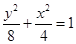 ,
, ;(2)存在定点
;(2)存在定点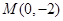 .
.
解析试题分析:(1)设出标准方程,由点的坐标代入求出基本量即得;(2)巧设直线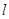 的方程为
的方程为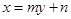 ,由直线与椭圆相切,求得
,由直线与椭圆相切,求得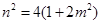 ,利用直线
,利用直线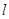 与
与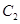 的准线相交求点
的准线相交求点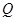 的坐标,写出以
的坐标,写出以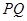 为直径的圆的方程,利用恒成立求解.
为直径的圆的方程,利用恒成立求解.
试题解析:(1)设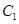 ,
,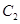 的标准方程为:
的标准方程为: ,
,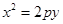 ,∵
,∵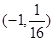 和
和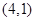 代入抛物线方程中得到的解相同,∴
代入抛物线方程中得到的解相同,∴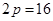 , (3分)
, (3分)
又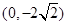 和
和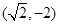 在椭圆上,把点的坐标代入椭圆方程得
在椭圆上,把点的坐标代入椭圆方程得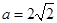 ,
,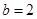 ,则
,则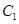 ,
,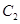
的标准方程分别为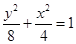 ,
, . (6分)
. (6分)
(2)设直线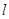 的方程为
的方程为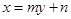 ,将其代入
,将其代入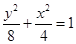 消去
消去 并化简整理得:
并化简整理得: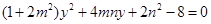 ,又直线与椭圆相切,
,又直线与椭圆相切,
∴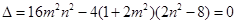 ,∴
,∴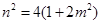 , (8分)
, (8分)
设切点 ,则
,则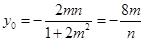 ,
,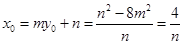 ,
,
又直线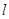 与
与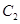 的准线
的准线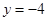 的交点
的交点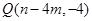 ,
,
∴以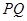 为直径的圆的方程为
为直径的圆的方程为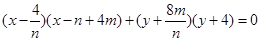 , (10分)
, (10分)
化简整理得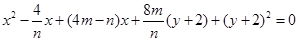 恒成立,
恒成立,
故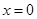 ,
, ,即存在定点
,即存在定点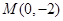 符合题意. (13分)
符合题意. (13分)
考点: 椭圆、抛物线的性质,圆的性质,直线与圆椭圆的关系,定点问题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
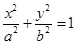 (a>b>0)的两个焦点和短轴的两个端点都在圆
(a>b>0)的两个焦点和短轴的两个端点都在圆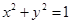 上.
上.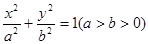 的左、右焦点分别为F1(-1,0),F2(1,0),过F1作与x轴不重合的直线l交椭圆于A,B两点.
的左、右焦点分别为F1(-1,0),F2(1,0),过F1作与x轴不重合的直线l交椭圆于A,B两点.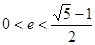 ,0为坐标原点,求证
,0为坐标原点,求证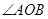 为钝角.
为钝角. 中,椭圆
中,椭圆 的右焦点为
的右焦点为 ,离心率为
,离心率为 .
. ,
, 的两条弦
的两条弦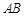 ,
, 相交于点
相交于点 (异于
(异于 ,
, 两点),且
两点),且 .
. ,
, 的斜率之和为定值.
的斜率之和为定值.
 的四个顶点恰好是一边长为2,一内角为
的四个顶点恰好是一边长为2,一内角为 的菱形的四个顶点.
的菱形的四个顶点.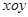 中,已知椭圆
中,已知椭圆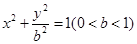 的左焦点为
的左焦点为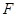 ,左、右顶点分别为
,左、右顶点分别为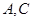 ,上顶点为
,上顶点为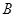 ,过
,过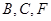 三点作圆
三点作圆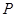
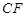 是圆
是圆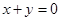 上,求椭圆的方程;
上,求椭圆的方程;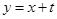 交(Ⅱ)中椭圆于
交(Ⅱ)中椭圆于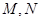 ,交
,交 轴于
轴于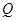 ,求
,求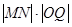 的最大值
的最大值 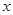 轴上的椭圆
轴上的椭圆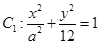 和双曲线
和双曲线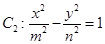 的离心率互为倒数,它们在第一象限交点的坐标为
的离心率互为倒数,它们在第一象限交点的坐标为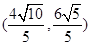 ,设直线
,设直线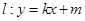 (其中
(其中 为整数).
为整数).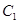 和双曲线
和双曲线 的标准方程;
的标准方程;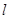 与椭圆
与椭圆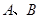 ,与双曲线
,与双曲线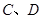 ,问是否存在直线
,问是否存在直线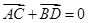 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由. 中,已知
中,已知 ,
, ,
, ,
, ,其中
,其中 .设直线
.设直线 与
与 的交点为
的交点为 ,求动点
,求动点 为参数)及普通方程.
为参数)及普通方程. 的顶点A在射线
的顶点A在射线 上,
上, 、
、 两点关于x轴对称,0为坐标原点,且线段AB上有一点M满足
两点关于x轴对称,0为坐标原点,且线段AB上有一点M满足 当点A在
当点A在 上移动时,记点M的轨迹为W.
上移动时,记点M的轨迹为W. 是否存在过
是否存在过 的直线
的直线 与W相交于P,Q两点,使得
与W相交于P,Q两点,使得 若存在,
若存在,