题目内容
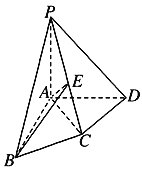
【题目】如图,在四棱锥![]() 中,PA⊥平面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.证明:
中,PA⊥平面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.证明:
(1)CD⊥AE;
(2)PD⊥平面ABE.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)关键证明CD⊥平面PAC,(2)关键证明AE⊥PD,AB⊥PD。
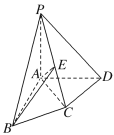
证明:(1)在四棱锥![]() 中,
中,
∵PA⊥平面ABCD,CD平面ABCD,
∴PA⊥CD.∵AC⊥CD,PA∩AC=A,
∴CD⊥平面PAC.
而AE平面PAC,∴CD⊥AE.
(2)由PA=AB=BC,∠ABC=60°,可得AC=PA.
∵E是PC的中点,∴AE⊥PC.
由(1)知AE⊥CD,且PC∩CD=C,
∴AE⊥平面PCD.
而PD平面PCD,∴AE⊥PD.
∵PA⊥平面ABCD,∴PA⊥AB.
又∵AB⊥AD且PA∩AD=A,
∴AB⊥平面PAD,而PD平面PAD,
∴AB⊥PD.
又∵AB∩AE=A,
∴PD⊥平面ABE.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
【题目】中国是世界互联网服务应用最好的国家,一部智能手机就可以跑遍国内所有地方,中国市场的移动支付普及率高得惊人.一家大型超市委托某高中数学兴趣小组调查该超市的顾客使用移动支付的情况,调查人员从年龄在![]() 内的顾客中,随机抽取了
内的顾客中,随机抽取了![]() 人,调查他们是否使用移动支付,结果如下表:
人,调查他们是否使用移动支付,结果如下表:
年龄 |
|
|
|
|
|
|
|
|
使用 |
|
|
|
|
|
|
|
|
不使用 |
|
|
|
|
|
|
|
|
(1)为更进一步推动移动支付,超市准备对使用移动支付的每位顾客赠送![]() 个环保购物袋,若某日该超市预计有
个环保购物袋,若某日该超市预计有![]() 人购物,试根据上述数据估计,该超市当天应准备多少个环保购物袋?
人购物,试根据上述数据估计,该超市当天应准备多少个环保购物袋?
(2)填写下面列联表,并根据列联表判断是否有![]() 的把握认为使用移动支付与年龄有关?
的把握认为使用移动支付与年龄有关?
年龄 | 年龄 | 小计 | |
使用移动支付 | |||
不使用移动支付 | |||
合计 |
附:下面的临界值表供参考:
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
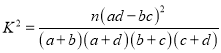 ,其中
,其中![]() .
.

