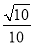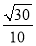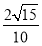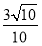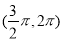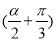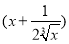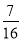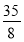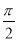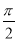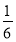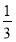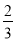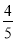Question

若函数f(x)对任意的实数x1，x2∈D，均有|f(x2)－f(x1)|≤|x2－x1|，则称函数f(x)是区间D上的“平缓函数”．

(1)判断g(x)＝sin x和h(x)＝x2－x是不是实数集R上的“平缓函数”，并说明理由；

(2)若数列{xn}对所有的正整数n都有|xn＋1－xn|≤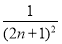，设yn＝sin xn，求证：|yn＋1－y1|＜.

 

Answer 1

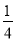（1）不是（2）见解析

【解析】g(x)＝sin x是R上的“平缓函数”，但h(x)＝x2－x不是区间R上的“平缓函数”．设φ(x)＝x－sin x，则φ′(x)＝1－cos x≥0，则φ(x)＝x－sin x是实数集R上的增函数，

不妨设x1＜x2，则φ(x1)＜φ(x2)，即x1－sin x1＜x2－sin x2，

则sin x2－sin x1＜x2－x1.①

又y＝x＋sin x也是R上的增函数，则x1＋sin x1＜x2＋sin x2，

即sin x2－sin x1＞x1－x2，②

由①②得－(x2－x1)＜sin x2－sin x1＜x2－x1.

∴|sin x2－sin x1|＜|x2－x1|对x1＜x2都成立．

当x1＞x2时，同理有|sin x2－sin x1|＜|x2－x1|成立．

又当x1＝x2时，|sin x2－sin x1|＝|x2－x1|＝0，

∴对任意的实数x1，x2∈R，

均有|sin x2－sin x1|≤|x2－x1|.

∴g(x)＝sin x是R上的“平缓函数”．

∵|h(x1)－h(x2)|＝|(x1－x2)(x1＋x2－1)|，

取x1＝3，x2＝2，则|h(x1)－h(x2)|＝4＞|x1－x2|，

∴h(x)＝x2－x不是R上的“平缓函数”．

(2)证明　由(1)得g(x)＝sin x是R上的“平缓函数”．

则|sin xn＋1－sin xn|≤|xn＋1－xn|，

∴|yn＋1－yn|≤|xn＋1－xn|.

而|xn＋1－xn|≤，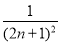

∴|yn＋1－yn|≤＜＝.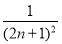

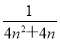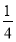
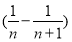∵|yn＋1－y1|＝|(yn＋1－yn)＋(yn－yn－1)＋(yn－1－yn－2)＋…＋(y2－y1)|，

∴|yn＋1－y1|≤|yn＋1－yn|＋|yn－yn－1|＋|yn－1－yn－2|＋…＋|y2－y1|.

∴|yn＋1－y1|≤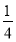

＝＜.
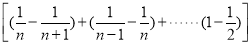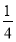
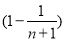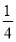