题目内容
如图,△ABC是圆O的内接三角形,AC=BC,D为圆O中 上一点,延长DA至点E,使得CE=CD.
上一点,延长DA至点E,使得CE=CD.
(1)求证:AE=BD;
(2)若AC⊥BC,求证:AD+BD=
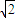 CD.
CD.
【答案】分析:(1)根据在△ABC、△ECD中∠ACE=∠BCD、CE=CD、AC=BC,可得到△ACE≌△BCD,再根据对应边相等得到AE=BD,得证.
(2)当AC⊥BC时,在△ECD中有∠ECD=90°,∠CED=∠CDE=45°,进而可得到DE=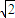 CD,再结合AD+BD=AD+EA=ED可知AD+BD=
CD,再结合AD+BD=AD+EA=ED可知AD+BD=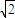 CD,从而得证.
CD,从而得证.
解答:证明:(1)在△ABC中,AC=BC∴∠CAB=∠CBA.
在△ECD中,CE=CD∴∠CED=∠CDE.
∵∠CBA=∠CDE,∴∠ACB=∠ECD.
∴∠ACB-∠ACD=∠ECD-∠ACD.
∴∠ACE=∠BCD.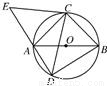
又CE=CD,AC=BC,
∴△ACE≌△BCD.
∴AE=BD.
(2)若AC⊥BC,
∵∠ACB=∠ECD,
∴∠ECD=90°,∠CED=∠CDE=45°.
∴DE=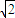 CD.
CD.
又∵AD+BD=AD+EA=ED,
∴AD+BD=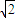 CD.
CD.
点评:本题主要考查三角形的全等和直线与圆的位置关系.高考对直线与圆的方程的考查以基础题为主,平时要多积累基础知识,这样到考试时才不会手忙脚乱.
(2)当AC⊥BC时,在△ECD中有∠ECD=90°,∠CED=∠CDE=45°,进而可得到DE=
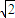 CD,再结合AD+BD=AD+EA=ED可知AD+BD=
CD,再结合AD+BD=AD+EA=ED可知AD+BD=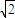 CD,从而得证.
CD,从而得证.解答:证明:(1)在△ABC中,AC=BC∴∠CAB=∠CBA.
在△ECD中,CE=CD∴∠CED=∠CDE.
∵∠CBA=∠CDE,∴∠ACB=∠ECD.
∴∠ACB-∠ACD=∠ECD-∠ACD.
∴∠ACE=∠BCD.

又CE=CD,AC=BC,
∴△ACE≌△BCD.
∴AE=BD.
(2)若AC⊥BC,
∵∠ACB=∠ECD,
∴∠ECD=90°,∠CED=∠CDE=45°.
∴DE=
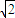 CD.
CD.又∵AD+BD=AD+EA=ED,
∴AD+BD=
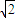 CD.
CD.点评:本题主要考查三角形的全等和直线与圆的位置关系.高考对直线与圆的方程的考查以基础题为主,平时要多积累基础知识,这样到考试时才不会手忙脚乱.

练习册系列答案
相关题目
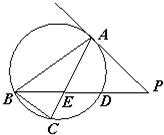 15、如图,△ABC是圆O的内接三角形,PA是圆O的切线,A为切点,PB交AC于点E,交圆O于点D,若PE=PA,∠ABC=60°,且PD=1,BD=8,则AC=
15、如图,△ABC是圆O的内接三角形,PA是圆O的切线,A为切点,PB交AC于点E,交圆O于点D,若PE=PA,∠ABC=60°,且PD=1,BD=8,则AC=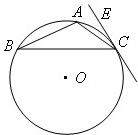 如图,△ABC是圆O的内接三角形,圆O的半径r=1,AB=1,BC=
如图,△ABC是圆O的内接三角形,圆O的半径r=1,AB=1,BC=
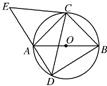
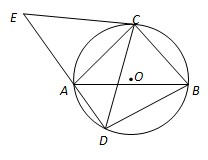 如图,△ABC是圆O的内接三角形,AC=BC,D为圆O中
如图,△ABC是圆O的内接三角形,AC=BC,D为圆O中 (几何证明选讲选做题)如图,ABC是圆O的内接等边三角形,AD⊥AB,与BC的延长线相交于D,与圆O相交于E.若圆O的半径r=1,则DE
(几何证明选讲选做题)如图,ABC是圆O的内接等边三角形,AD⊥AB,与BC的延长线相交于D,与圆O相交于E.若圆O的半径r=1,则DE