题目内容
 (几何证明选讲选做题)如图,ABC是圆O的内接等边三角形,AD⊥AB,与BC的延长线相交于D,与圆O相交于E.若圆O的半径r=1,则DE
(几何证明选讲选做题)如图,ABC是圆O的内接等边三角形,AD⊥AB,与BC的延长线相交于D,与圆O相交于E.若圆O的半径r=1,则DE2
2
.分析:连接OA,OB,由ABC是圆O的内接等边三角形,AD⊥AB,圆O的半径r=1,知∠AOB=120°,∠D=30°,∠BAD=90°,故AB=BC=CD=
,AD=3,由
×2
=DE×3,能求出DE.
| 3 |
| 3 |
| 3 |
解答: 解:连接OA,OB,
解:连接OA,OB,
∵ABC是圆O的内接等边三角形,AD⊥AB,圆O的半径r=1,
∴∠AOB=120°,∠D=30°,∠BAD=90°,
∴AB=
=
,
BC=CD=
,
AD=
=3,
∴
×2
=DE×3,
∴DE=2.
故答案为:2.
 解:连接OA,OB,
解:连接OA,OB,∵ABC是圆O的内接等边三角形,AD⊥AB,圆O的半径r=1,
∴∠AOB=120°,∠D=30°,∠BAD=90°,
∴AB=
| 1+1-2×1×1×cos120° |
| 3 |
BC=CD=
| 3 |
AD=
(2
|
∴
| 3 |
| 3 |
∴DE=2.
故答案为:2.
点评:本题考查与圆有关的比例线段的应用,是基础题.解题时要认真审题,注意切割线定理的合理运用.

练习册系列答案
相关题目
 (几何证明选讲选做题)
(几何证明选讲选做题) (几何证明选讲选做题)如图,四边形ABCD内接于⊙O,AB为⊙O的直径,直线MN切⊙O于D,∠MDA=60°,则∠BCD=
(几何证明选讲选做题)如图,四边形ABCD内接于⊙O,AB为⊙O的直径,直线MN切⊙O于D,∠MDA=60°,则∠BCD= (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (几何证明选讲选做题)
(几何证明选讲选做题)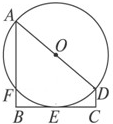 (几何证明选讲选做题)
(几何证明选讲选做题)