题目内容
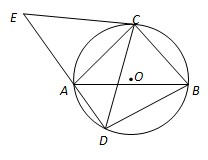如图，△ABC是圆O的内接三角形，AC=BC，D为圆O中 | AB |
分析：证明AE=BD，可证明△ACE≌△BCD，利用AAS可证．
解答：证明：
，∴∠BAC=∠ABC
∵∠BAC=∠BDC，∠ABC=∠ADC
∴∠ADC=∠BDC，
∵CE=CD，∠ADC=∠E
∴∠E=∠BDC，…（4分）
∵四边形ADBC内接于圆O，∴∠CAE=∠CBD，…（6分）
又AC=BC，∴△ACE≌△BCD，∴AE=BD． …（10分）
|
∵∠BAC=∠BDC，∠ABC=∠ADC
∴∠ADC=∠BDC，
∵CE=CD，∠ADC=∠E
∴∠E=∠BDC，…（4分）
∵四边形ADBC内接于圆O，∴∠CAE=∠CBD，…（6分）
又AC=BC，∴△ACE≌△BCD，∴AE=BD． …（10分）
点评：本题以圆为载体，考查三角形的全等，关键是利用圆的内接四边形的性质．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
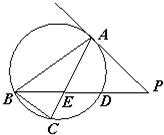15、如图，△ABC是圆O的内接三角形，PA是圆O的切线，A为切点，PB交AC于点E，交圆O于点D，若PE=PA，∠ABC=60°，且PD=1，BD=8，则AC=
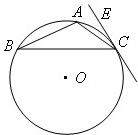如图，△ABC是圆O的内接三角形，圆O的半径r=1，AB=1，BC=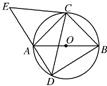
（几何证明选讲选做题）如图，ABC是圆O的内接等边三角形，AD⊥AB，与BC的延长线相交于D，与圆O相交于E．若圆O的半径r=1，则DE