题目内容
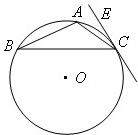 如图,△ABC是圆O的内接三角形,圆O的半径r=1,AB=1,BC=
如图,△ABC是圆O的内接三角形,圆O的半径r=1,AB=1,BC=| 2 |
分析:本题首先根据三角形的正弦定理求得∠CBA的度数,再根据弦切角的度数等于它所夹的弧的所对的圆周角进行求解.
解答:解:在三角形ABC中,AB=OA=OB=1,
∴∠BOA=60°,
∴∠BCA=30°,
在三角形ABC中,由正弦定理得:
=
,
代入数据得:sin∠BAC=
=
,
∴∠BAC=135°,
从而∠ACE=15°.
故填:15°
∴∠BOA=60°,
∴∠BCA=30°,
在三角形ABC中,由正弦定理得:
| AB |
| sin∠ACB |
| BC |
| sin∠BAC |
代入数据得:sin∠BAC=
| ||
| 1 |
| ||
| 2 |
∴∠BAC=135°,
从而∠ACE=15°.
故填:15°
点评:此题综合考查了弦切角定理和三角形的正弦定理,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
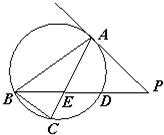 15、如图,△ABC是圆O的内接三角形,PA是圆O的切线,A为切点,PB交AC于点E,交圆O于点D,若PE=PA,∠ABC=60°,且PD=1,BD=8,则AC=
15、如图,△ABC是圆O的内接三角形,PA是圆O的切线,A为切点,PB交AC于点E,交圆O于点D,若PE=PA,∠ABC=60°,且PD=1,BD=8,则AC=
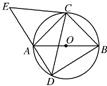
 如图,△ABC是圆O的内接三角形,AC=BC,D为圆O中
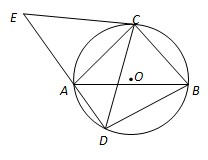
如图,△ABC是圆O的内接三角形,AC=BC,D为圆O中 (几何证明选讲选做题)如图,ABC是圆O的内接等边三角形,AD⊥AB,与BC的延长线相交于D,与圆O相交于E.若圆O的半径r=1,则DE
(几何证明选讲选做题)如图,ABC是圆O的内接等边三角形,AD⊥AB,与BC的延长线相交于D,与圆O相交于E.若圆O的半径r=1,则DE