题目内容
8.已知椭圆E的中心在原点,焦点在坐标轴上,且经过两点M(-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$)和N(1,$\frac{\sqrt{2}}{2}$).(1)求椭圆E的标准方程;
(2)设F为椭圆的右焦点,过点F作斜率为1的直线l交椭圆于AB两点,以AB为直径的圆O交y轴于P、Q两点,劣弧长PQ记为d,求$\frac{d}{|AB|}$的值.
分析 (1)通过设椭圆E的标准方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,代入两点M(-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$)和N(1,$\frac{\sqrt{2}}{2}$)计算即得结论;
(2)通过(1)可知直线l方程为x-y-1=0,并与椭圆方程联立可知A(0,-1)、B($\frac{4}{3}$,$\frac{1}{3}$),进而可求出P(0,-1)、Q(0,$\frac{1}{3}$),计算即得结论.
解答 解:(1)设椭圆E的标准方程为:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,
则$\left\{\begin{array}{l}{\frac{1}{2{a}^{2}}+\frac{3}{4{b}^{2}}=1}\\{\frac{1}{{a}^{2}}+\frac{1}{2{b}^{2}}=1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{a}^{2}=2}\\{{b}^{2}=1}\end{array}\right.$,
∴椭圆E的标准方程为:$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(2)由(1)可知F(1,0),则直线l方程为:x-y-1=0,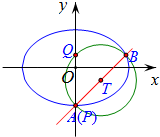
联立直线与椭圆方程,消去y整理可知:3x2-4x=0,
解得:x=0或x=$\frac{4}{3}$,
不妨记A(0,-1)、B($\frac{4}{3}$,$\frac{1}{3}$),则线段AB的中点T($\frac{2}{3}$,-$\frac{1}{3}$),
∴AT=$\sqrt{(0-\frac{2}{3})^{2}+(-1+\frac{1}{3})^{2}}$=$\frac{2\sqrt{2}}{3}$,
设Q(0,y),则QT=$\frac{2\sqrt{2}}{3}$,即$\sqrt{(0-\frac{2}{3})^{2}+(y+\frac{1}{3})^{2}}$=$\frac{2\sqrt{2}}{3}$,
解得:y=$\frac{1}{3}$或y=-1,
记P(0,-1)、Q(0,$\frac{1}{3}$),则d=$\frac{1}{4}$•2π•AT,
∴$\frac{d}{|AB|}$=$\frac{\frac{π}{2}AT}{2AT}$=$\frac{π}{4}$.
点评 本题考查直线与圆锥曲线的关系,考查数形结合能力,注意解题方法的积累,属于中档题.

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案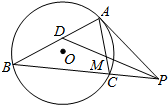 如图所示,△ABC内接于圆O,过点A的切线交BC的延长线于点P,D为AB的中点,DP交AC于点M,若BP=8,AM=4,AC=6,则PA=( )
如图所示,△ABC内接于圆O,过点A的切线交BC的延长线于点P,D为AB的中点,DP交AC于点M,若BP=8,AM=4,AC=6,则PA=( )| A. | 4$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | 5$\sqrt{2}$ |
 如图,圆O内切于△ABC的边于点D,E,F,AB=AC,连结AD交圆O于点H,直线HF交BC的延长线于点G.
如图,圆O内切于△ABC的边于点D,E,F,AB=AC,连结AD交圆O于点H,直线HF交BC的延长线于点G.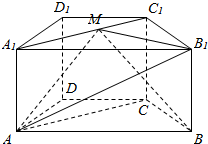 在四棱柱ABCD-A1B1C1D1中,底面ABCD为梯形,AB∥CD,AD=DC=CB=1,∠ABC=$\frac{π}{3}$,对角面A1ACC1为矩形,平面A1ACC1⊥平面ABCD,CC1=1.
在四棱柱ABCD-A1B1C1D1中,底面ABCD为梯形,AB∥CD,AD=DC=CB=1,∠ABC=$\frac{π}{3}$,对角面A1ACC1为矩形,平面A1ACC1⊥平面ABCD,CC1=1. 在圆O中,AB,CD是互相平行的两条弦,直线AE与圆O相切于点A,且与CD的延长线交于点E,求证:AD2=AB•ED.
在圆O中,AB,CD是互相平行的两条弦,直线AE与圆O相切于点A,且与CD的延长线交于点E,求证:AD2=AB•ED.