题目内容
12 3
4 5 6
7 8 9 10
11 12 13 14 15
…
根据以上规律,数阵中第n(n≥3)行的从左至右的第3个数是 .
【答案】分析:先找到数的分布规律,求出第n行结束的时候一共出现的数的个数,再求第n+1行从左向右的第3个数即可.
解答:解:由排列的规律可得,第n-1行结束的时候排了1+2+3+…+(n-1)=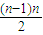 个数.
个数.
所以n行从左向右的第3个数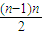 +3=
+3=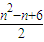 .
.
故答案为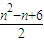 .
.
点评:本题借助于一个三角形数阵考查了数列的应用,是道基础题.
解答:解:由排列的规律可得,第n-1行结束的时候排了1+2+3+…+(n-1)=
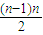 个数.
个数.所以n行从左向右的第3个数
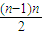 +3=
+3=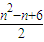 .
.故答案为
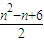 .
.点评:本题借助于一个三角形数阵考查了数列的应用,是道基础题.

练习册系列答案
相关题目
2、计算机中常用十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与十进制的数的对应关系如下表:
|
为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽出取14件和5件,测量产品中的微量元素x,y的含量(单位:毫克).下表是乙厂的5件产品的测量数据:
(1)已知甲厂生产的产品共有98件,求乙厂生产的产品总数.
(2)当产品中的微量元素x,y满足x≥175,y≥75,该产品为优等品.用上述样本数据估计乙厂生产的优等品的数量.
(3)从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中的优等品数ξ的分布列及其均值(即数学期望).
| 编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 178 | 166 | 175 | 180 |
| y | 75 | 80 | 77 | 70 | 81 |
(2)当产品中的微量元素x,y满足x≥175,y≥75,该产品为优等品.用上述样本数据估计乙厂生产的优等品的数量.
(3)从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中的优等品数ξ的分布列及其均值(即数学期望).
班主任为了对本班学生的考试成绩进行分析,决定从全班25名女同学,15名男同学中随机抽取一个容量为8的样本进行分析.若这8位同学的数学、物理分数对应如下表:
根据如表数据用变量y与x的相关关系
(1)画出样本的散点图,并说明物理成绩y与数学成绩x之间是正相关还是负相关?
(2)求y与x的线性回归直线方程(系数精确到0.01),并指出某个学生数学83分,物理约为多少分?
参考公式:回归直线的方程是:
=bx+a,
其中b=
,a=
-b
;其中
i是与xi对应的回归估计值.
参考数据:
=77.5,
=85,
(x1-
)2≈1050,
(x1-
)(y1-
)≈688.
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
(1)画出样本的散点图,并说明物理成绩y与数学成绩x之间是正相关还是负相关?
(2)求y与x的线性回归直线方程(系数精确到0.01),并指出某个学生数学83分,物理约为多少分?
参考公式:回归直线的方程是:
| ? |
| y |
其中b=
| |||||||
|
. |
| y |
. |
| x |
| ? |
| y |
参考数据:
. |
| x |
. |
| y |
| 8 |
 |
| i=1 |
. |
| x |
| 8 |
 |
| i=1 |
. |
| x |
. |
| y |
下表给出了两组变量X与Y、U与V相对应的两组数据,r1表示变量Y与X之间的线性相关系数,r2表示变量V与U之间的线性相关系数,则( )
| X | 10 | 11.3 | 11.8 | 12.5 | 13 |
| Y | 1 | 2 | 3 | 4 | 5 |
| U | 10 | 11.3 | 11.8 | 12.5 | 13 |
| V | 5 | 4 | 3 | 2 | 1 |
| A、r2<r1<0 |
| B、0<r2<r1 |
| C、r2<0<r1 |
| D、r2=r1 |