题目内容
设函数f(x)=| 3 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 3 |
| 1 |
| 2 |
(I)求函数f(x)的最小正周期及单调递减区间;
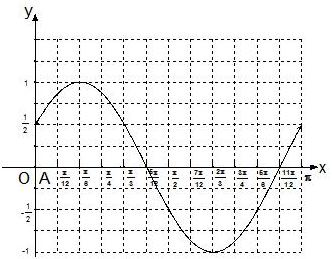
(II)作出y=f(x)在x∈[0,π]上的图象.(不要求书写作图过程)
分析:(1)逆用正弦和余弦的二倍角公式来降幂,用辅角公式把三角函数整理成Asin(ωx+φ)的形式,得到周期和单调递减区间,最后结果要写成区间的形式.
(2)根据所给的变量的范围,得到三角函数的值域,由最大值与最小值的和为
,求出字母系数a,在坐标系中用五点法做出函数的图象,坐标系的几个元素不要忽略.
(2)根据所给的变量的范围,得到三角函数的值域,由最大值与最小值的和为
| 1 |
| 2 |
解答:解:(I)∵f(x)=
sin2x+
+a-
=sin(2x+
)+a,
∴T=π,
由
+2kπ≤2x+
≤
+2kπ,
得
+kπ ≤x≤
+kπk∈z
故函数f(x)的单调递减区间是[
+kπ,
+kπ]k∈z.
 (II)∵-
(II)∵-
≤x≤
,
∴-
≤ 2x+
≤
,
∴-
≤sin(2x+
)≤1
当x∈[-
,
]时,
原函数的最大值与最小值的和-
+a+1+a=
,
解得a=0.
∴f(x)=sin(2x+
),图象如图.
| ||
| 2 |
| 1+cos2x |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
∴T=π,
由
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
得
| π |
| 6 |
| 2π |
| 3 |
故函数f(x)的单调递减区间是[
| π |
| 6 |
| 2π |
| 3 |
 (II)∵-
(II)∵-| π |
| 6 |
| π |
| 3 |
∴-
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴-
| 1 |
| 2 |
| π |
| 6 |
当x∈[-
| π |
| 6 |
| π |
| 3 |
原函数的最大值与最小值的和-
| 1 |
| 2 |
| 1 |
| 2 |
解得a=0.
∴f(x)=sin(2x+
| π |
| 6 |
点评:本题综合考查三角函数的变换和性质,包括周期、单调性、函数的值域、函数的图象,这是一个综合题目,也是高考必考的一种类型的题目,属于容易题,是一个送分的题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目