Question

【题目】已知函数f（x）= x2+2ax，g（x）=3a2lnx+b，设两曲线y=f（x），y=g（x）有公共点，且在该点处的切线相同，则a∈（0，+∞）时，实数b的最大值是（ ）
A.
B.
C.
D.

Answer 1

【答案】D
【解析】解：函数f（x）的导数为f'（x）=x+2a， 函数g（x）的导数为 ，
由于两曲线y=f（x），y=g（x）有公共点，设为P（x0 ， y0），
则 ，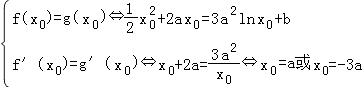
由于x0＞0，a＞0
则x0=a，因此
构造函数 ，
由h'（t）=2t（1﹣3lnt），
当 时，h'（t）＞0即h（t）单调递增；当 时，h'（t）＜0即h（t）单调递减，
则 即为实数b的最大值．
故选D．
分别求出函数f（x）的导数，函数g（x）的导数．由于两曲线y=f（x），y=g（x）有公共点，
设为P（x0 ， y0），则有f（x0）=g（x0），且f′（x0）=g′（x0），解出x0=a，得到b关于a的函数，构造函数 ，运用导数求出单调区间和极值、最值，即可得到b的最大值．