题目内容
(本题满分12分)在 中,内角
中,内角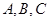 的对边分别为
的对边分别为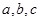 ,已知
,已知
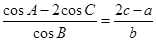
(1)求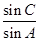 的值;
的值;
(2)若 求
求 的面积S。
的面积S。
 中,内角
中,内角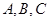 的对边分别为
的对边分别为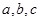 ,已知
,已知 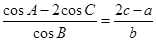
(1)求
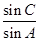 的值;
的值; (2)若
 求
求 的面积S。
的面积S。(1)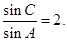 ; (2)
; (2)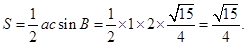
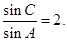 ; (2)
; (2)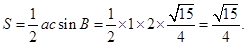
本试题主要是考查了解三角形中的正弦定理和余弦定理的运用,以及三角形面积公式的运用。
(1)利用正弦定理,化边为角得到关系与三角关系式,得到sinC=2sinA,得到c=2a,
(2)根据余弦定理得到b的值,进而结合三角形面积公式求解面积。
解:(1)由正弦定理,设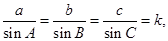
则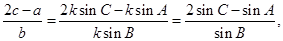 所以
所以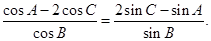
即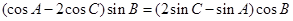 ,化简可得
,化简可得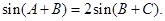
又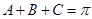 ,所以
,所以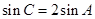 因此
因此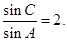
(2)由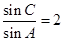 得
得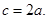
由余弦定理
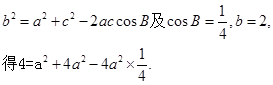 解得a=1因此c="2" 又因为
解得a=1因此c="2" 又因为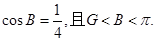
所以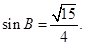 因此
因此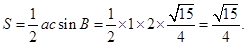
(1)利用正弦定理,化边为角得到关系与三角关系式,得到sinC=2sinA,得到c=2a,
(2)根据余弦定理得到b的值,进而结合三角形面积公式求解面积。
解:(1)由正弦定理,设
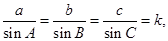
则
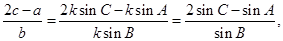 所以
所以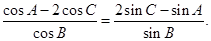
即
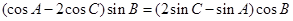 ,化简可得
,化简可得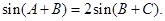
又
 ,所以
,所以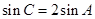 因此
因此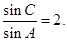
(2)由
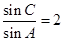 得
得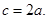
由余弦定理
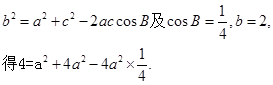 解得a=1因此c="2" 又因为
解得a=1因此c="2" 又因为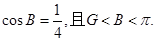
所以
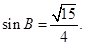 因此
因此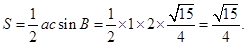

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
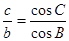 ,则此三角形为( )
,则此三角形为( ) 中, 内角
中, 内角 所对的边分别是
所对的边分别是 .已知
.已知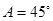 ,
,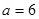 ,
, 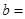
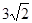 ,则
,则 的大小为
的大小为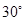
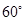
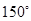
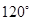
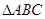 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为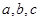 ,且满足
,且满足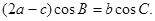
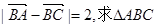 的面积的最大值.
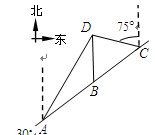
的面积的最大值.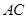 是佛山市一环东线的一段,其中
是佛山市一环东线的一段,其中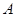 、
、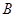 、
、 分别是林上路、佛陈路、花卉大道出口,经测量陈村花卉世界
分别是林上路、佛陈路、花卉大道出口,经测量陈村花卉世界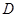 位于点
位于点 方向
方向 处,位于点
处,位于点 方向上,并且
方向上,并且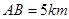 .
.
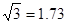 ,
,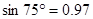 ,
,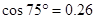 ,
, ,
, ,
, 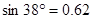 ,
,
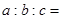
 方向,距离12 nmile的海面上有一走私船C正以10 nmile/h的速度沿东偏南
方向,距离12 nmile的海面上有一走私船C正以10 nmile/h的速度沿东偏南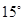 方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东
方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东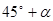 的方向去追,.求追及所需的时间和
的方向去追,.求追及所需的时间和 角的正弦值.
角的正弦值.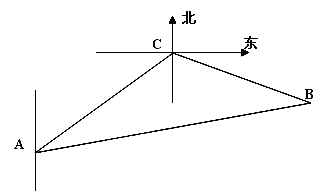
 中,
中,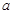 ,
,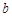 ,
,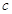 是角
是角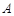 ,
,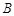 ,
,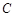 的对边,且
的对边,且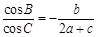
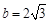 ,求
,求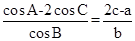 .
.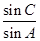 的值;
的值;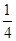 ,△
,△