题目内容
【题目】已知某中学高三文科班学生共有800人参加了数学与地理的水平测试，现从中随机抽取100人的数学与地理的水平测试成绩如下表：
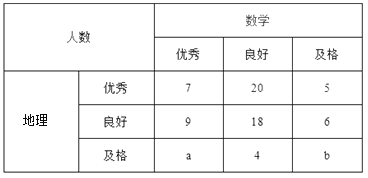
成绩分为优秀、良好、及格三个等级；横向，纵向分别表示地理成绩与数学成绩，例如：表中数学成绩为良好的共有
.
（Ⅰ）若在该样本中，数学成绩优秀率是30％，求
的值；
（Ⅱ）已知
，求数学成绩为优秀的人数比及格的人数少的概率.
【答案】（Ⅰ）
、
；（Ⅱ）
.
【解析】试题分析: （Ⅰ）根据优秀率定义,由样本中数学成绩优秀率,可得关于
的等式,解得 的值; （Ⅱ）由（Ⅰ）知
,又
，可列出所有满足条件的情况,找出其中数学成绩为优秀的人数比及格的人数少的组数,利用古典概型的定义,可求得所要求概率.
试题解析:（Ⅰ）由题意得，
，解得，
∵
，
∴.
（Ⅱ）由题意，知，且，
∴满足条件的
有:
，
，
共14组，且每组出现的可能性相同.
其中数学成绩为优秀的人数比及格的人数少有:
共6组.
∴数学成绩为优秀的人数比及格的人数少的概率为
.
练习册系列答案
阅读快车系列答案
相关题目
【题目】某研究小组在电脑上进行人工降雨模拟实验，准备用
、
、
三种人工降雨方式分别对甲、乙、丙三地实施人工降雨，其试验数据统计如表：
方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验总次数 |
| 甲 | 4次 | 6次 | 2次 | 12次 |
| 乙 | 3次 | 6次 | 3次 | 12次 |
| 丙 | 2次 | 2次 | 8次 | 12次 |
假定对甲、乙、丙三地实施的人工降雨彼此互不影响，请你根据人工降雨模拟实验的统计数据：
（Ⅰ）求甲、乙、丙三地都恰为中雨的概率；
（Ⅱ）考虑到旱情和水土流失，如果甲地恰需中雨即达到理想状态，乙地必须是大雨才达到理想状态，丙地只能是小雨或中雨即达到理想状态，记“甲、乙、丙三地中达到理想状态的个数”为随机变量
，求随机变量的分布列和数学期望
．
