题目内容
数列{an}的通项公式 (
( ),若前n项的和
),若前n项的和 ,则项数n为
,则项数n为
A.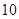 | B.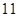 | C.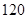 | D.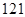 |
C
解析试题分析:根据题意,由于数列{an}的通项公式 ,根据累加法可知,前n项的和
,根据累加法可知,前n项的和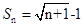 ,因此可知
,因此可知 =
=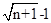 ,n=120,故可知答案为C.
,n=120,故可知答案为C.
考点:数列的通项公式
点评:主要是考查了数列的求和的运用,属于基础题。

练习册系列答案
相关题目
设数列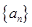 满足
满足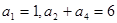 ,且对任意
,且对任意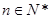 ,函数
,函数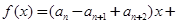
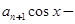
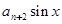 满足
满足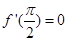 ,若
,若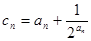 ,则数列
,则数列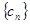 的前
的前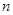 项和
项和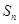 为( )
为( )
A.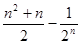 | B.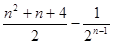 |
C.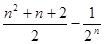 | D. |
若数列 满足
满足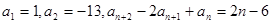 ,则当
,则当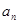 取最小值时
取最小值时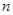 的值为( )
的值为( )
A.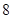 或 或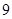 | B.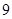 | C.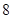 | D. 或 或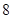 |
已知数列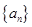 满足
满足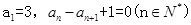 则此数列中
则此数列中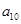 等于
等于
| A.-7 | B.11 | C.12 | D.-6 |
已知函数 的图象在点
的图象在点 处的切线的斜率为3,数列
处的切线的斜率为3,数列
的前 项和为
项和为 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
已知数列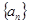 满足:
满足: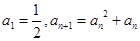 ,则
,则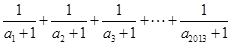 的值所在区间是( )
的值所在区间是( )
A.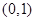 | B.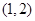 | C. | D.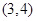 |
已知数列 的首项
的首项 ,且
,且 ,则
,则 为( )
为( )
| A.7 | B.15 | C.30 | D.31 |
已知数列{ }满足
}满足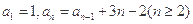 ,则
,则 的通项公式为( )
的通项公式为( )
A.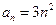 |
B. |
C.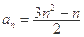 |
D.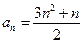 |
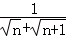 ,若前n项和为6,则n= _________ .
,若前n项和为6,则n= _________ .