题目内容
已知实数a≠0,函数f(x)=ax(x-2)2(x∈R)(Ⅰ)若函数f(x)有极大值32,求实数a的值;
(Ⅱ)若对于x∈[-2,1],不等式f(x)<
| 32 | 9 |
分析:(Ⅰ)首先求出函数的导函数,利用导数作为工具解决函数的极值问题,注意方程思想的运用;
(Ⅱ)将恒成立问题转化为函数的最值问题是解决该题的关键.利用导数作为工具求出函数在给出区间上的最值,再列出不等式进行求解.
(Ⅱ)将恒成立问题转化为函数的最值问题是解决该题的关键.利用导数作为工具求出函数在给出区间上的最值,再列出不等式进行求解.
解答:解:(Ⅰ)由题意f(x)=ax3-4ax2+4ax,故f'(x)=3ax2-8ax+4a=a(3x-2)(x-2),
令f'(x)=0解得x=2或x=
,
∵f(x)有极大值32,
而f(2)=0
∴f(
)=32,代入原函数解出a=27.
(Ⅱ)f'(x)=a(3x-2)(x-2),由f′(x)=0得出x=2或x=
.列表如下:
当a>0时,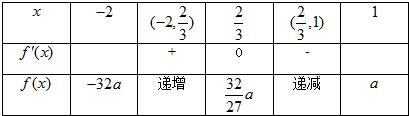 f(x)max=f(
f(x)max=f(
)=
a<
?a<3,∴0<a<3
当a<0时,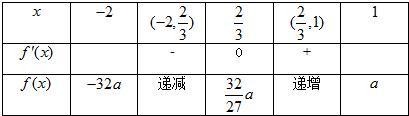
∴f(x)max=-32a<
?a>-
,∴-
<a<0
综上a∈(-
,0)∪(0,3).
令f'(x)=0解得x=2或x=
| 2 |
| 3 |
∵f(x)有极大值32,
而f(2)=0
∴f(
| 2 |
| 3 |
(Ⅱ)f'(x)=a(3x-2)(x-2),由f′(x)=0得出x=2或x=
| 2 |
| 3 |
当a>0时,
 f(x)max=f(
f(x)max=f(| 2 |
| 3 |
| 32 |
| 27 |
| 32 |
| 9 |
当a<0时,

∴f(x)max=-32a<
| 32 |
| 9 |
| 1 |
| 9 |
| 1 |
| 9 |
综上a∈(-
| 1 |
| 9 |
点评:本题考查函数与导数的综合问题,考查导数作为工具解决函数的问题,注意函数的极值与函数导数的关系,恒成立问题转化为函数最值问题的转化与化归思想.通过解不等式求出字母取值范围的化归思想.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目