题目内容

函数f(x)=Asin(ωx+?)(A＞0，ω＞0，|?|＜
π
2
)的一段图象如图所示．
（1）求函数y=f（x）的解析式；
（2）将函数y=f（x）的图象向右平移
π
8
个单位，得到y=g（x）的图象，求直线y=
6
与函数y=
2
g(x)的图象在（0，π）内所有交点的坐标．
分析：（1）通过函数的图象的最大值求出A，函数的周期求出ω，然后求解φ，即可求函数y=f（x）的解析式；
（2）通过函数y=f（x）的图象向右平移
π
8
个单位，得到y=g（x）的图象，然后联立直线y=
6
与函数y=
2
g(x)得到方程，即可求解在（0，π）内所有交点的坐标．
解答：解：（1）由图知A=2，T=π，于是ω=
2π
T
=2
将y=2sin 2x的图象向左平移
π
12
，
得y=2sin（2x+φ）的图象．
于是φ=2•
π
12
=
π
6
，
∴f（x）=2sin\b\lc\(\rc\)(\a\vs4\al\co1(2x+
π
6
))．
（2）依题意得
g（x）=2sin[2(x-
π
8
)+
π
6
]
．=2sin（2x-
π
12
）．
故y=
2
g（x）=2
2
sin（2x-
π
12
）．
由
y=
6
y=2
2
sin(2x-
π
12
)

得sin（2x-
π
12
）=
3
2
．…（8分）
∴2x-
π
12
=
π
3
+2kπ或2x-
π
12
=
2π
3
+2kπ（k∈Z），
∴x=
5π
24
+kπ或x=
3π
8
+kπ（k∈Z）．
∵x∈（0，π），
∴x=
5π
24
或x=
3π
8
．…（11分）
∴交点坐标为(
5π
24
，
6
)，(
3π
8
，
6
)．
点评：本题考查三角函数的解析式的求法，函数的图象的交点 的求法考查计算能力．
练习册系列答案
相关题目
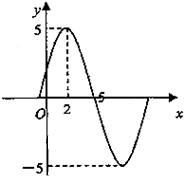精英家教网已知函数f(x)=Asin(ωx+φ)(A＞0，ω＞0，|φ|＜
π2
)的部分图象如图所示．
（1）求函数f（x）的解析式；
（2）若图象g（x）与函数f（x）的图象关于点P（4，0）对称，求函数g（x）的单调递增区间．
（2013•大连一模）已知函数f(x)=Asin(ωx+φ)(x∈R，A＞0，ω＞0，|φ|＜
π
2
)的图象（部分）如图所示，则ω，φ分别为（　　）
当x∈[-
π
6
，
2π
3
]时，函数f(x)=Asin(ωx+θ) (A＞0，ω＞0，|θ|＜
π
2
)的图象如图所示．
（1）求函数f（x）在[-
π
6
，
2π
3
]上的表达式；
（2）求方程f(x)=
2
2
在[-
π
6
，
2π
3
]的解集．
精英家教网函数f(x)=Asin(ωx+φ)，x∈R(A＞0，ω＞0，|φ|＜
π
2
)的一段图象如图5所示：将y=f（x）的图象向右平移m（m＞0）个单位，可得到函数y=g（x）的图象，且图象关于原点对称，g(
π
2013
)＞0．
（1）求A、ω、φ的值；
（2）求m的最小值，并写出g（x）的表达式；
（3）若关于x的函数y=g(
tx
2
)在区间[-
π
3
，
π
4
]上最小值为-2，求实数t的取值范围．
精英家教网已知函数f(x)=Asin(ωx+φ)(A＞0，ω＞0，x∈R，|φ|＜
π
2
)的图象（部分）如图所示，则f（x）的解析式是（　　）
A、f(x)=5sin(
π
3
x+
π
6
)
B、f(x)=5sin(
π
6
x-
π
6
)
C、f(x)=5sin(
π
6
x+
π
6
)
D、f(x)=5sin(
π
3
x-
π
6
)

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网