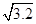题目内容
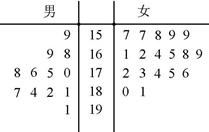
某银行柜台设有一个服务窗口,假设顾客办理业务所需的时间互相独立,且都是整数分钟,对以往顾客办理业务所需的时间统计结果如下:

从第一个顾客开始办理业务时计时。
(1)估计第三个顾客恰好等待4分钟开始办理业务的概率;
(2)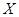 表示至第2分钟末已办理完业务的顾客人数,求
表示至第2分钟末已办理完业务的顾客人数,求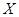 的分布列及数学期望
的分布列及数学期望

从第一个顾客开始办理业务时计时。
(1)估计第三个顾客恰好等待4分钟开始办理业务的概率;
(2)
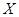 表示至第2分钟末已办理完业务的顾客人数,求
表示至第2分钟末已办理完业务的顾客人数,求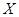 的分布列及数学期望
的分布列及数学期望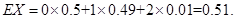
【考点定位】本题主要考察离散型随机变量的概率、概率分布与期望,同时考察逻辑思维能力、推理论证能力数据处理能力等,是常考考点
设顾客办理业务所需时间,Y,用频率估计概率的分布列如下
(1)事件“第三个顾客恰好等待4分钟开始办理业务”记作A,则
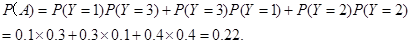
(2)X所有可能取值为0,1,2.所以P(X=0)=P(Y>2)=0.5;
P(X=1)=P(Y=1)P(Y>1)+P(Y=2)=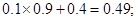
P(X=2)=P(Y=1)P(Y=1)=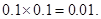 因此X的分布列为:
因此X的分布列为:
所以X的期望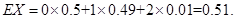
| Y | 1 | 2 | 3 | 4 | 5 |
| P | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
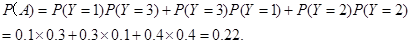
(2)X所有可能取值为0,1,2.所以P(X=0)=P(Y>2)=0.5;
P(X=1)=P(Y=1)P(Y>1)+P(Y=2)=
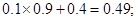
P(X=2)=P(Y=1)P(Y=1)=
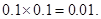 因此X的分布列为:
因此X的分布列为:| X | 0 | 1 | 2 |
| P | 0.5 | 0.49 | 0.01 |

练习册系列答案
相关题目
 表示取到次品的个数,则
表示取到次品的个数,则 等于( )
等于( )


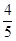 ,第二、第三种产品受欢迎的概率分别为
,第二、第三种产品受欢迎的概率分别为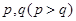 ,且不同种产品是否受欢迎相互独立.记
,且不同种产品是否受欢迎相互独立.记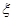 为公司向市场投放三种新型产品受欢迎的数量,其分布列为
为公司向市场投放三种新型产品受欢迎的数量,其分布列为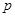
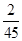
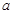
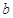
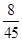
 的值
的值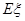 .
.
 表示所选代表中女“运动健将”的人数,试写出
表示所选代表中女“运动健将”的人数,试写出 班参加高考体检,
班参加高考体检, 个班中,任选
个班中,任选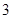 个班先参加视力检查. (I)求这
个班先参加视力检查. (I)求这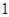 个班班级序号是偶数的概率;
个班班级序号是偶数的概率;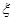 为这
为这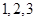 班,则有两组相邻的,
班,则有两组相邻的,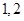 班和
班和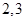 班,此时
班,此时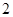 ).求随机变量
).求随机变量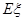 .
.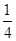 ,不堵车的概率为
,不堵车的概率为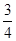 ;汽车走公路②堵车的概率为
;汽车走公路②堵车的概率为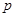 ,不堵车的概率为
,不堵车的概率为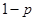 ,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。(I)若三辆车中恰有一辆车被堵的概率为
,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。(I)若三辆车中恰有一辆车被堵的概率为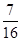 ,求走公路②堵车的概率;(Ⅱ)在(I)的条件下,求三辆车中被堵车辆的个数
,求走公路②堵车的概率;(Ⅱ)在(I)的条件下,求三辆车中被堵车辆的个数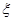 的分布列和数学期望。
的分布列和数学期望。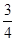
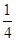
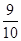
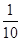
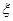 表示取出的竹签的最大号码,则
表示取出的竹签的最大号码,则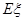 的值是
的值是 .
.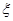 的分布列为下表所示:
的分布列为下表所示: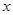
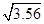 C.3.2 D.
C.3.2 D.