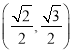题目内容
【题目】已知双曲线
的离心率为2，左右焦点分别为
，
，过右焦点且垂直于x轴的直线与双曲线交于A，B两点，且
的周长为
．
（1）求双曲线C的方程；
（2）已知直线
，点P是双曲线C上的动点，求点P到直线l的距离的最小值．
【答案】（1）
；（2）最小值为
【解析】
（1）根据题意可得
，
，根据周长可得
，结合
，求解可得
，
，所以曲线C的方程为：
；
（2）求出与l平行且与C相切的直线，利用平行直线间距离公式可得最小值．
（1）由题得
，所以，，
又
，所以
，
，
，
因为
的周长为
，
所以①，
又因为②，
①－②，得
，
即
，解得，，
所以曲线C的方程为：；
（2）设与直线
平行且与C相切的直线方程为
，
由
得
，
则
，解得
．
设点P到直线l的距离为d，则根据平行线间的距离公式可得，
，
所以当
时，d取最小值为.
练习册系列答案
备战中考寒假系列答案
相关题目
