题目内容
.给出以下四个结论:
①函数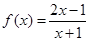 的对称中心是
的对称中心是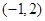 ;
;
②若关于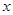 的方程
的方程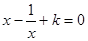 在
在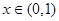 没有实数根,则
没有实数根,则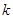 的取值范围是
的取值范围是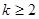 ;
;
③在△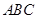 中,“
中,“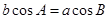 ”是“△
”是“△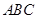 为等边三角形”的必要不充分条件;
为等边三角形”的必要不充分条件;
④若将函数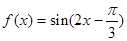 的图像向右平移
的图像向右平移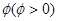 个单位后变为偶函数,则
个单位后变为偶函数,则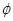 的最小值是
的最小值是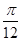 ;其中正确的结论是:
;其中正确的结论是:
①函数
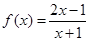 的对称中心是
的对称中心是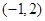 ;
;②若关于
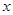 的方程
的方程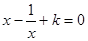 在
在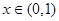 没有实数根,则
没有实数根,则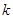 的取值范围是
的取值范围是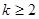 ;
;③在△
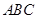 中,“
中,“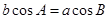 ”是“△
”是“△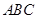 为等边三角形”的必要不充分条件;
为等边三角形”的必要不充分条件;④若将函数
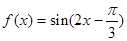 的图像向右平移
的图像向右平移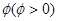 个单位后变为偶函数,则
个单位后变为偶函数,则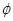 的最小值是
的最小值是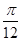 ;其中正确的结论是:
;其中正确的结论是: ①③④
解:因为
①函数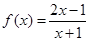 的对称中心是
的对称中心是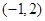 ;成立
;成立
②若关于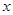 的方程
的方程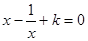 在
在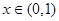 没有实数根,则
没有实数根,则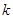 的取值范围是
的取值范围是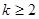 ;不成立
;不成立
③在△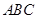 中,“
中,“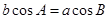 ”是“△
”是“△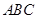 为等边三角形”的必要不充分条件;成立
为等边三角形”的必要不充分条件;成立
④若将函数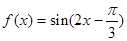 的图像向右平移
的图像向右平移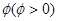 个单位后变为偶函数,则
个单位后变为偶函数,则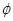 的最小值是
的最小值是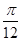 ,成立
,成立
①函数
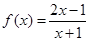 的对称中心是
的对称中心是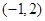 ;成立
;成立②若关于
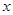 的方程
的方程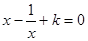 在
在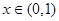 没有实数根,则
没有实数根,则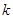 的取值范围是
的取值范围是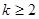 ;不成立
;不成立③在△
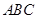 中,“
中,“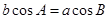 ”是“△
”是“△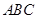 为等边三角形”的必要不充分条件;成立
为等边三角形”的必要不充分条件;成立④若将函数
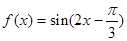 的图像向右平移
的图像向右平移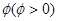 个单位后变为偶函数,则
个单位后变为偶函数,则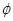 的最小值是
的最小值是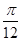 ,成立
,成立
练习册系列答案
相关题目
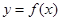 是幂函数,则函数
是幂函数,则函数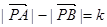 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;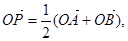 则动点P的轨迹为
则动点P的轨迹为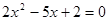 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率; 有相同的焦点.
有相同的焦点.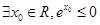
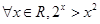
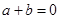 的充要条件是
的充要条件是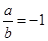
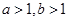 是
是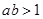 的充分条件
的充分条件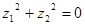 ,则复数
,则复数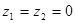
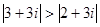
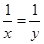 ,则
,则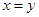
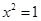 ,则
,则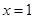
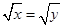
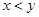 ,则
,则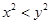
 中至少有一个大于0
中至少有一个大于0 
 一定也是0
一定也是0
 ,使得
,使得 ”为假命题,则实数
”为假命题,则实数 的范围 .
的范围 .