题目内容
已知抛物线 .命题p: 直线l1:
.命题p: 直线l1: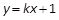 与抛物线C有公共点.命题q: 直线l2:
与抛物线C有公共点.命题q: 直线l2: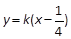 被抛物线C所截得的线段长大于2.若
被抛物线C所截得的线段长大于2.若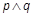 为假,
为假, 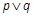 为真,求k的取值范围.
为真,求k的取值范围.
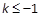 或
或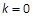 或
或 .
.
解析试题分析:先求出p为真, 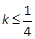 ;q为真,得
;q为真,得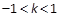 且
且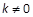 .
.
由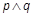 为假,
为假, 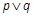 为真可得:p,q一真一假.若p真q假, 则
为真可得:p,q一真一假.若p真q假, 则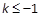 或
或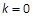 ;若q真p假, 则
;若q真p假, 则 .
.
综上可得结论.
若p为真,联立C和l1的方程化简得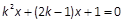 .
.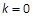 时,方程显然有解;
时,方程显然有解;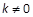 时,由
时,由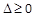 得
得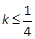 且
且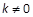 . 综上
. 综上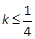 (4分)
(4分)
若q为真, 联立C和l2的方程化简得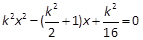 ,
,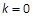 时显然不成立;∴
时显然不成立;∴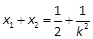 ,
,
由于l2是抛物线的焦点弦, 故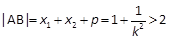 ,解得
,解得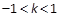 且
且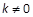 .(8分)
.(8分)
∵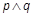 为真,
为真, 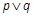 为假,∴p,q一真一假.
为假,∴p,q一真一假.
若p真q假, 则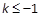 或
或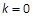 ; 若q真p假, 则
; 若q真p假, 则 .
.
综上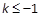 或
或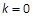 或
或 . (12分)
. (12分)
考点:复合命题真假的判断;根与系数的关系;焦点弦问题.

练习册系列答案
相关题目
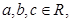 则“
则“ ”是“
”是“ ”成立的充分不必要条件;
”成立的充分不必要条件; 时,函数
时,函数 的最小值为2;
的最小值为2; ”与命题“
”与命题“ 或
或 ”都是真命题,则命题
”都是真命题,则命题 ,则
,则 .
.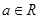 ,命题
,命题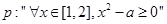 ,命题
,命题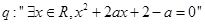 .⑴若命题
.⑴若命题 为真命题,求实数
为真命题,求实数 的取值范围;⑵若命题
的取值范围;⑵若命题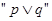 为真命题,命题
为真命题,命题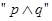 为假命题,求实数
为假命题,求实数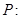 函数
函数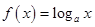 在区间
在区间 上是单调递增函数;命题
上是单调递增函数;命题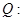 不等式
不等式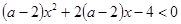 对任意实数
对任意实数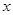 恒成立.若
恒成立.若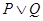 是真命题,且
是真命题,且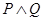 为假命题,求实数
为假命题,求实数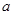 的取值范围.
的取值范围. :实数
:实数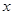 满足
满足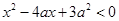 ,其中
,其中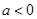 ,命题
,命题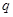 :实数
:实数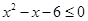 或
或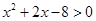 ,且
,且 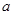 的取值范围.
的取值范围.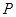 :复数
:复数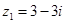 ,复数
,复数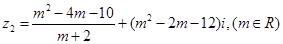 ,
, 是虚数;命题
是虚数;命题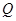 :关于
:关于 的方程
的方程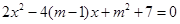 的两根之差的绝对值小于
的两根之差的绝对值小于 ;若
;若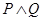 为真命题,求实数
为真命题,求实数 的取值范围.
的取值范围. B”; w ②“若x2+y2=0,则x,y全为0”的否命题;
B”; w ②“若x2+y2=0,则x,y全为0”的否命题;