题目内容
已知函数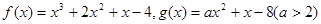 .
.
(1)求函数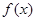 的极值;
的极值;
(2)若对任意的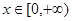 ,都有
,都有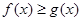 ,求实数a的取值范围.
,求实数a的取值范围.
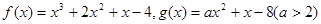 .
.(1)求函数
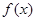 的极值;
的极值;(2)若对任意的
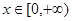 ,都有
,都有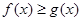 ,求实数a的取值范围.
,求实数a的取值范围.(1)当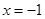 ,
,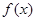 取得极大值为-4,当
取得极大值为-4,当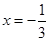 时,
时,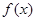 取得极小值为
取得极小值为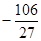
(2)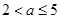
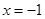 ,
,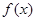 取得极大值为-4,当
取得极大值为-4,当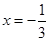 时,
时,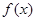 取得极小值为
取得极小值为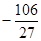
(2)
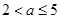
(1)由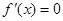 可得极值点,再根据极值点左正右负为极大值点,极值点左负右正是极小值点.确定极大值和极小值.
可得极值点,再根据极值点左正右负为极大值点,极值点左负右正是极小值点.确定极大值和极小值.
(II)本小题本质是构造函数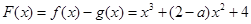 然后利用导数求其在
然后利用导数求其在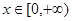 上最小值,根据最小值大于或等于零解关于a的不等式即可求出a的取值范围
上最小值,根据最小值大于或等于零解关于a的不等式即可求出a的取值范围
(1)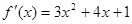 ,令
,令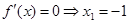 或
或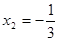 ……2分
……2分
令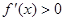 ,得
,得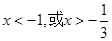 ,…………3分
,…………3分
即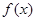 在
在 上为增函数,在
上为增函数,在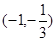 上为增函数;…………4分
上为增函数;…………4分
故当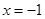 ,
,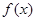 取得极大值为-4,当
取得极大值为-4,当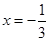 时,
时,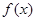 取得极小值为
取得极小值为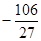 ……5分
……5分
(2)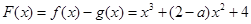 ………………6分
………………6分
当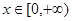 ,
,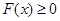 恒成立
恒成立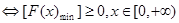 …………7分
…………7分
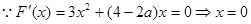 或
或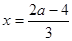 ………………8分
………………8分
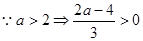 ……………………………………9分
……………………………………9分
当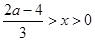 时,
时,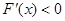 ; 当
; 当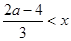 时,
时,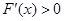 …………10分
…………10分
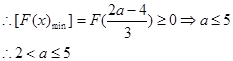
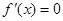 可得极值点,再根据极值点左正右负为极大值点,极值点左负右正是极小值点.确定极大值和极小值.
可得极值点,再根据极值点左正右负为极大值点,极值点左负右正是极小值点.确定极大值和极小值.(II)本小题本质是构造函数
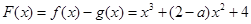 然后利用导数求其在
然后利用导数求其在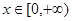 上最小值,根据最小值大于或等于零解关于a的不等式即可求出a的取值范围
上最小值,根据最小值大于或等于零解关于a的不等式即可求出a的取值范围(1)
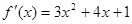 ,令
,令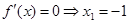 或
或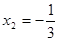 ……2分
……2分令
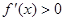 ,得
,得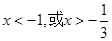 ,…………3分
,…………3分即
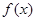 在
在 上为增函数,在
上为增函数,在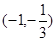 上为增函数;…………4分
上为增函数;…………4分故当
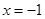 ,
,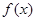 取得极大值为-4,当
取得极大值为-4,当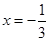 时,
时,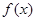 取得极小值为
取得极小值为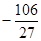 ……5分
……5分(2)
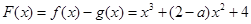 ………………6分
………………6分当
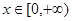 ,
,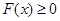 恒成立
恒成立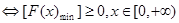 …………7分
…………7分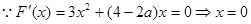 或
或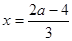 ………………8分
………………8分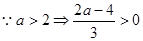 ……………………………………9分
……………………………………9分当
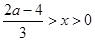 时,
时,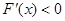 ; 当
; 当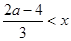 时,
时,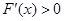 …………10分
…………10分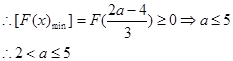

练习册系列答案
相关题目
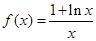
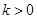 且函数
且函数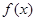 在区间
在区间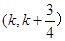 上存在极值,求实数
上存在极值,求实数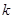 的取值范围;
的取值范围;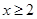 时,不等式
时,不等式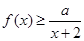 恒成立,求实数
恒成立,求实数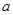 的取值范围;
的取值范围;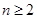 ,
,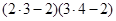 ……
……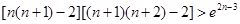 .
.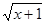 )的定义域是[0,3],则函数f(x)的定义域是 .
)的定义域是[0,3],则函数f(x)的定义域是 .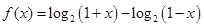 (16分)
(16分)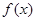 的定义域;
的定义域; ,
, ,则
,则 的最大值为 .
的最大值为 .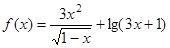 的定义域是 ;
的定义域是 ;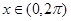 时,函数
时,函数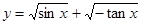 的定义域是 。
的定义域是 。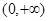 的是( )
的是( )