题目内容
已知在平面直角坐标系中的一个椭圆,它的中心在原点,左焦点为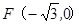 ,且过点
,且过点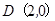 .
.
(1)求该椭圆的标准方程;
(2)设点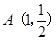 ,若
,若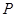 是椭圆上的动点,求线段
是椭圆上的动点,求线段 的中点
的中点 的轨迹方程.
的轨迹方程.
【答案】
(1) 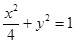 . (2)
. (2) 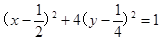 .
.
【解析】
试题分析:(1)由已知得椭圆的半长轴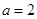 ,半焦距
,半焦距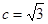 ,则半短轴
,则半短轴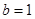 .
3分
.
3分
又椭圆的焦点在 轴上, ∴椭圆的标准方程为
轴上, ∴椭圆的标准方程为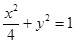 .
5分
.
5分
(2)设线段 的中点为
的中点为 ,点
,点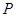 的坐标是
的坐标是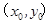 ,
,
由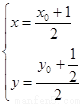 ,得
,得 ,
9分
,
9分
由点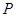 在椭圆上,得
在椭圆上,得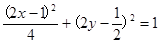 ,
11分
,
11分
∴线段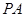 中点
中点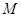 的轨迹方程是
的轨迹方程是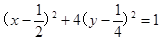 .
12分
.
12分
考点:本题考查了椭圆的标准方程及轨迹方程的求法
点评:若动点P(x,y)随已知曲线上的点Q(x0,y0)的变动而变动,且x0、y0可用x、y表示,则将Q点坐标表达式代入已知曲线方程,即得点P的轨迹方程.这种方法称为相关点法(或代换法).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目