Question

11．某几何体的三视图如图所示（其中主视图和左视图相同），则该几何体的体积为（　　）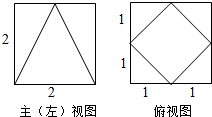

• A． $\frac{17}{2}$
• B． $\frac{20}{3}$
• C． $\frac{16}{3}$
• D． $\frac{25}{4}$

Answer 1

分析 由已知中的三视力可得该几何体是一个正方体切去四个三棱锥所得的组合体，结合正方体和棱锥体积公式，可得答案．

解答 解：由已知中的三视力可得该几何体是一个正方体切去四个三棱锥所得的组合体，
正方体的体积为：2×2×2=8，
每个三棱锥的体积为：$\frac{1}{3}×\frac{1}{2}×1×1×2$=$\frac{1}{3}$，
故组合体的体积V=8-$\frac{1}{3}×4$=$\frac{20}{3}$，
故选：B

点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．