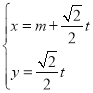题目内容
【题目】已知数列![]() 中,
中,![]() ,点
,点![]() (
(![]() )在直线y = x上,
)在直线y = x上,
(Ⅰ)计算a2,a3,a4的值;
(Ⅱ)令bn=an+1﹣an﹣1,求证:数列{bn}是等比数列;
(Ⅲ)设Sn、Tn分别为数列{an}、{bn}的前n项和,是否存在实数λ,使得数列![]() 为等差数列?若存在,试求出λ的值;若不存在,请说明理由.
为等差数列?若存在,试求出λ的值;若不存在,请说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析;(Ⅲ)存在λ=2.
;(Ⅱ)见解析;(Ⅲ)存在λ=2.
【解析】试题分析:(1)根据点![]() 在直线
在直线![]() 上,可得
上,可得![]() ,代入计算可得
,代入计算可得![]() 的值;(2)利用
的值;(2)利用![]() ,及
,及![]() ,即可证明数列
,即可证明数列![]() 是等比数列;(3)求得数列的前三项,求得
是等比数列;(3)求得数列的前三项,求得![]() ,再验证即可求得结论.
,再验证即可求得结论.![]()
试题解析:(Ⅰ)由题意,∵点(n,2an+1﹣an)在直线y=x上,
∴2an+1﹣an=n
∵![]() ,∴
,∴![]() ,
,
同理,![]() ,
,![]() ;
;
(Ⅱ)证明:∵bn=an+1﹣an﹣1,2an+1﹣an=n
∴bn+1=an+2﹣an+1﹣1=![]() ﹣an+1﹣1=
﹣an+1﹣1=![]() (an+1﹣an﹣1)=
(an+1﹣an﹣1)=![]() bn,
bn,
∵b1=a2﹣a1﹣1=﹣![]()
∴数列{bn}是以﹣![]() 为首项,
为首项,![]() 为公比的等比数列;
为公比的等比数列;
(Ⅲ)解:存在λ=2,使数列![]() 是等差数列.
是等差数列.
由(Ⅱ)知,![]() ,
,![]() ,
,
∵an+1=n﹣1﹣bn=n﹣1+![]() ,∴an=n﹣2+
,∴an=n﹣2+![]() ,
,
∴Sn= =
=![]()
由题意,要使数列![]() 是等差数列,则
是等差数列,则![]()
∴2×![]() =
=![]() ﹣
﹣![]() λ+
λ+![]() ,∴λ=2
,∴λ=2
当λ=2时,![]() =
=![]() ,数列是等差数列
,数列是等差数列
∴当且仅当λ=2时,数列是等差数列.

练习册系列答案
相关题目