题目内容
已知抛物线C:y2=2px(p>0),其焦点是椭圆mx2+4y2=1的右焦点,且椭圆的离心率为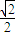 .
.(Ⅰ)试求抛物线C的方程;
(Ⅱ)在y轴上截距为2的直线l与抛物线C交于M,N两点,以线段MN为直径的圆过原点,求直线l的方程;
(Ⅲ)若以原点为圆心,以t(t>0)为半径的圆分别交抛物线C上半支和y轴正半轴于A,B两点,直线AB与x轴交于点Q,试用A点的横坐标x表示点Q的坐标.
【答案】分析:(Ⅰ)利用椭圆的离心率,求出m,可得右焦点坐标,从而可求抛物线C的方程;
(Ⅱ)设直线l的方程与抛物线联立,利用以线段MN为直径的圆过原点,结合向量知识,即可求直线l的方程;
(Ⅲ)确定A、B的坐标,可得直线的方程,令y=0,即可求得结论.
解答:解:(Ⅰ)∵椭圆mx2+4y2=1的离心率为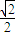 ,
,
∴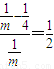 ,∴m=2
,∴m=2
∴2x2+4y2=1的右焦点坐标为( ,0)
,0)
∵抛物线C:y2=2px(p>0),其焦点是椭圆mx2+4y2=1的右焦点,
∴抛物线C的方程为y2=2x;
(Ⅱ)由题意,设l的方程为y=kx+2,设M(x1,y1)、N(x2,y2),
直线方程代入抛物线方程可得k2x2+(4k-2)x+4=0,则x1+x2=-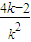 ,x1x2=
,x1x2=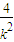
∴y1y2=8-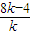
∵以线段MN为直径的圆过原点,∴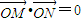
∴x1x2+y1y2=0
∴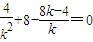
∴k=-1
∴l的方程为y=-x+2,即x+y-2=0;
(Ⅲ)设圆的方程为x2+y2=t,与抛物线方程联立,可得x2+2x-t=0
设A(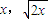 ),则t=x2+2x,B(0,x2+2x)
),则t=x2+2x,B(0,x2+2x)
∴直线AB的方程为y-(x2+2x)=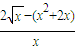 (x-0)
(x-0)
令y=0,则x=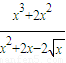 .
.
∴Q( ,0)
,0)
点评:本题以抛物线为载体,考查抛物线的几何性质,考查向量知识的运用,考查学生分析解决问题的能力,综合性强.
(Ⅱ)设直线l的方程与抛物线联立,利用以线段MN为直径的圆过原点,结合向量知识,即可求直线l的方程;
(Ⅲ)确定A、B的坐标,可得直线的方程,令y=0,即可求得结论.
解答:解:(Ⅰ)∵椭圆mx2+4y2=1的离心率为
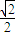 ,
,∴
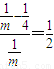 ,∴m=2
,∴m=2∴2x2+4y2=1的右焦点坐标为(
 ,0)
,0)∵抛物线C:y2=2px(p>0),其焦点是椭圆mx2+4y2=1的右焦点,
∴抛物线C的方程为y2=2x;
(Ⅱ)由题意,设l的方程为y=kx+2,设M(x1,y1)、N(x2,y2),
直线方程代入抛物线方程可得k2x2+(4k-2)x+4=0,则x1+x2=-
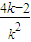 ,x1x2=
,x1x2=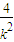
∴y1y2=8-
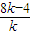
∵以线段MN为直径的圆过原点,∴
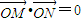
∴x1x2+y1y2=0
∴
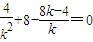
∴k=-1
∴l的方程为y=-x+2,即x+y-2=0;
(Ⅲ)设圆的方程为x2+y2=t,与抛物线方程联立,可得x2+2x-t=0
设A(
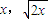 ),则t=x2+2x,B(0,x2+2x)
),则t=x2+2x,B(0,x2+2x)∴直线AB的方程为y-(x2+2x)=
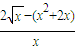 (x-0)
(x-0)令y=0,则x=
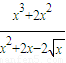 .
.∴Q(
 ,0)
,0)点评:本题以抛物线为载体,考查抛物线的几何性质,考查向量知识的运用,考查学生分析解决问题的能力,综合性强.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知抛物线C:y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4且位于x轴上方的点. A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M(O为坐标原点).
如图,已知抛物线C:y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4且位于x轴上方的点. A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M(O为坐标原点). 已知抛物线C:y2=4x,点M(m,0)在x轴的正半轴上,过M的直线l与C相交于A、B两点,O为坐标原点.
已知抛物线C:y2=4x,点M(m,0)在x轴的正半轴上,过M的直线l与C相交于A、B两点,O为坐标原点.