题目内容
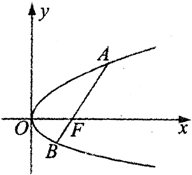 已知抛物线y2=2px(p>0)过焦点F的任一条弦AB,设A(x1,y1),B(x2,y2)且y1>0,y2<0
已知抛物线y2=2px(p>0)过焦点F的任一条弦AB,设A(x1,y1),B(x2,y2)且y1>0,y2<0(1)若y1y2=-4,求抛物线方程;
(2)是否存在常数λ,使
| 1 |
| |FA| |
| 1 |
| |FB| |
(3)在抛物线对称轴(ox的正方向)上是否存在一定点M,经过点M的任意一条弦AB,使
| 1 |
| |MA|2 |
| 1 |
| |MB|2 |
分析:(1)先设AB的方程代入y2=2px,利用条件y1y2=-4,可求抛物线方程;(2)利用抛物线的定义表示出FA,FB,再进行求解;(3)设AB:x=ty+p代入y2=2px,从而表示出MA2=(1+t2)y12,MB2=(1+t2)y22,进而得证.
解答:解:(1)设AB:x=ty+
代入y2=2px,得y2-2py-p2=0,∴y1y2=-p2=-4,∴p=2,∴抛物线方程y2=4x;
(2)①当AB⊥x轴时,
+
=λ=
②一般地,FA=
+x1=
,FB=
+x2=
∴
+
=
=-
=
;
(3)假设存在定点M(x0,0)(x0>0)
①当AB⊥x轴时,可得
+
=-
,M(p,0)
②一般地,设AB:x=ty+p代入y2=2px,得y2-2pty-2p2=0,∴y1y2=-2p2,y1+y2=2pt,
∵MA2=(1+t2)y12,MB2=(1+t2)y22,∴
+
=-
得证.
| p |
| 2 |
(2)①当AB⊥x轴时,
| 1 |
| |FA| |
| 1 |
| |FB| |
| 2 |
| p |
②一般地,FA=
| p |
| 2 |
| y1(y1-y2) |
| 2p |
| p |
| 2 |
| y2(y2-y1) |
| 2p |
| 1 |
| |FA| |
| 1 |
| |FB| |
| 2p(y2-y1) |
| y1y2(y1-y2) |
| 2p |
| y1y2 |
| 2 |
| p |
(3)假设存在定点M(x0,0)(x0>0)
①当AB⊥x轴时,可得
| 1 |
| |MA|2 |
| 1 |
| |MB|2 |
| 1 |
| p2 |
②一般地,设AB:x=ty+p代入y2=2px,得y2-2pty-2p2=0,∴y1y2=-2p2,y1+y2=2pt,
∵MA2=(1+t2)y12,MB2=(1+t2)y22,∴
| 1 |
| |MA|2 |
| 1 |
| |MB|2 |
| 1 |
| p2 |
点评:本题主要考查是否存在性命题,通常可以借助于特殊情形,猜想结论,再进行一般性德证明,要充分利用抛物线过焦点弦的性质.

练习册系列答案
相关题目