题目内容
已知直线l:y=ax+1-a(a∈R).若存在实数a使得一条曲线与直线l有两个不同的交点,且以这两个交点为端点的线段长度恰好等于|a|,则称此曲线为直线l的“绝对曲线”.下面给出四条曲线方程:①y="-2"
|x-1|;②y=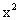 ;③(x-1)2+(y-1)2=1;④x2+3y2=4;则其中直线l的“绝对曲线”有
;③(x-1)2+(y-1)2=1;④x2+3y2=4;则其中直线l的“绝对曲线”有
A.①④ B.②③ C.②④ D.②③④
【答案】
D
【解析】
试题分析:根据题意,由于直线l:y=ax+1-a(a∈R).若存在实数a使得一条曲线与直线l有两个不同的交点,且以这两个交点为端点的线段长度恰好等于|a|,则称此曲线为直线l的“绝对曲线”,那么对于选项①y="-2"
|x-1|;与l:y=ax+1-a联立方程组,由于解方程可知不满足题意,由于②y=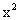 与l:y=ax+1-a联立方程组可知弦长为|a|成立。;同理对于③(x-1)2+(y-1)2=1;④x2+3y2=4;分别加以验证可知,那么能满足题意的曲线有②③④,故选D.
与l:y=ax+1-a联立方程组可知弦长为|a|成立。;同理对于③(x-1)2+(y-1)2=1;④x2+3y2=4;分别加以验证可知,那么能满足题意的曲线有②③④,故选D.
考点:直线与圆锥曲线的交点
点评:主要是考查了直线与圆锥曲线的 位置关系的运用,属于中档题。

练习册系列答案
相关题目
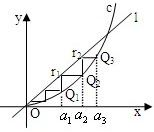 设a>0,如图,已知直线l:y=ax及曲线C:y=x2,C上的点Q1的横坐标为a1(0<a1<a).从C上的点Qn(n≥1)作直线平行于x轴,交直线l于点Pn+1,再从点Pn+1作直线平行于y轴,交曲线C于点Qn+1.Qn(n=1,2,3,…)的横坐标构成数列{an}.
设a>0,如图,已知直线l:y=ax及曲线C:y=x2,C上的点Q1的横坐标为a1(0<a1<a).从C上的点Qn(n≥1)作直线平行于x轴,交直线l于点Pn+1,再从点Pn+1作直线平行于y轴,交曲线C于点Qn+1.Qn(n=1,2,3,…)的横坐标构成数列{an}.