题目内容
已知直线l:y=ax+b,其中实数a,b∈{-1,1,2}.
(Ⅰ)求可构成的不同的直线l的条数;
(Ⅱ)求直线l:y=ax+b与圆x2+y2=1没有公共点的概率.
(Ⅰ)求可构成的不同的直线l的条数;
(Ⅱ)求直线l:y=ax+b与圆x2+y2=1没有公共点的概率.
分析:(Ⅰ)实数a,b∈{-1,1,2},直线l:y=ax+b,由加法计数原理能求出可构成的不同的直线l的条数.
(Ⅱ)直线l:y=ax+b与圆x2+y2=1没有公共点,是指圆心(0,0)到直线ax-y+b=0的距离大于圆的半径,由此能直线l:y=ax+b与圆x2+y2=1没有公共点的概率.
(Ⅱ)直线l:y=ax+b与圆x2+y2=1没有公共点,是指圆心(0,0)到直线ax-y+b=0的距离大于圆的半径,由此能直线l:y=ax+b与圆x2+y2=1没有公共点的概率.
解答:解:(Ⅰ)∵实数a,b∈{-1,1,2},直线l:y=ax+b,
∴可构成的不同的直线l的条数有:
a=-1,b=-1,1,2;a=1,b=-1,1,2;a=2,b=-1,1,2.
故可构成的不同的直线l的条数共9条.
(Ⅱ)直线l:y=ax+b与圆x2+y2=1没有公共点,
是指圆心(0,0)到直线ax-y+b=0的距离d=
>圆的半径1,
即
>1,即a2+1<b2,
∵构成直线l:y=ax+b的(a,b)的值有(-1,-1),(-1,1),(-1,2),(1,-1),
(1,1),(1,2),(2,-1),(2,1),(2,2),
满足a2+1<b2的(a,b)的值有(-1,2),(1,2),
∴直线l:y=ax+b与圆x2+y2=1没有公共点的概率P=
.
∴可构成的不同的直线l的条数有:
a=-1,b=-1,1,2;a=1,b=-1,1,2;a=2,b=-1,1,2.
故可构成的不同的直线l的条数共9条.
(Ⅱ)直线l:y=ax+b与圆x2+y2=1没有公共点,
是指圆心(0,0)到直线ax-y+b=0的距离d=
| |b| | ||
|
即
| |b| | ||
|
∵构成直线l:y=ax+b的(a,b)的值有(-1,-1),(-1,1),(-1,2),(1,-1),
(1,1),(1,2),(2,-1),(2,1),(2,2),
满足a2+1<b2的(a,b)的值有(-1,2),(1,2),
∴直线l:y=ax+b与圆x2+y2=1没有公共点的概率P=
| 2 |
| 9 |
点评:本题考查直线的条数的求法,考查直线与圆没有公共点的概率,解题时要认真审题,注意加法计数原理和点到直线的距离公式的合理运用.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
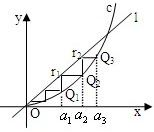 设a>0,如图,已知直线l:y=ax及曲线C:y=x2,C上的点Q1的横坐标为a1(0<a1<a).从C上的点Qn(n≥1)作直线平行于x轴,交直线l于点Pn+1,再从点Pn+1作直线平行于y轴,交曲线C于点Qn+1.Qn(n=1,2,3,…)的横坐标构成数列{an}.
设a>0,如图,已知直线l:y=ax及曲线C:y=x2,C上的点Q1的横坐标为a1(0<a1<a).从C上的点Qn(n≥1)作直线平行于x轴,交直线l于点Pn+1,再从点Pn+1作直线平行于y轴,交曲线C于点Qn+1.Qn(n=1,2,3,…)的横坐标构成数列{an}.