题目内容
已知直线l:y=ax+1与双曲线C:3x2-y2=1相交于A、B两点.
(1)求实数a的取值范围;
(2)当实数a取何值时,以线段AB为直径的圆经过坐标原点.
(1)求实数a的取值范围;
(2)当实数a取何值时,以线段AB为直径的圆经过坐标原点.
分析:(1)把直线与双曲线方程联立消去y,利用二次项非0,且判别式大于0求得a的范围.
(2)把直线l的方程与双曲线的方程联立消去y,根据判别式大于0求得a的范围,根据OA⊥OB,推断出y1y2=-x1x2.根据韦达定理表示出x1x2.进而根据直线方程表示出y1y2,代入y1y2=-x1x2.求得a.
(2)把直线l的方程与双曲线的方程联立消去y,根据判别式大于0求得a的范围,根据OA⊥OB,推断出y1y2=-x1x2.根据韦达定理表示出x1x2.进而根据直线方程表示出y1y2,代入y1y2=-x1x2.求得a.
解答:解(1)联立方程组
,得(3-a2)x2-2ax-2=0. …(2分)
∵直线l与曲线C有两个交点A、B,
∴
,即
. …(4分)
∴实数a的取值范围是-
<a<
且a≠±
. …(5分)
(2)设点A、B的坐标为(x1,y1)、(x2,y2). …(6分)
由(1)可知,
.
∵以线段AB为直径的圆经过原点,
∴
⊥
,即x1x2+y1y2=0. …(8分)
又y1=ax1+1,y2=ax2+1,
∴x1x2+(ax1+1)(ax2+1)=0,
即(a2+1)•
+a•
+1=0,解得a=±1(都满足(1)求出的条件) …(11分)
∴a=±1时,以线段AB为直径的圆经过坐标原点. …(12分)
|
∵直线l与曲线C有两个交点A、B,
∴
|
|
∴实数a的取值范围是-
| 6 |
| 6 |
| 3 |
(2)设点A、B的坐标为(x1,y1)、(x2,y2). …(6分)
由(1)可知,
|
∵以线段AB为直径的圆经过原点,
∴
| OA |
| OB |
又y1=ax1+1,y2=ax2+1,
∴x1x2+(ax1+1)(ax2+1)=0,
即(a2+1)•
| -2 |
| 3-a2 |
| 2a |
| 3-a2 |
∴a=±1时,以线段AB为直径的圆经过坐标原点. …(12分)
点评:本题主要考查了双曲线的简单性质,直线与双曲线的位置关系.考查了学生综合分析问题和推理的能力,基本的运算能力.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
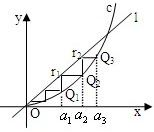 设a>0,如图,已知直线l:y=ax及曲线C:y=x2,C上的点Q1的横坐标为a1(0<a1<a).从C上的点Qn(n≥1)作直线平行于x轴,交直线l于点Pn+1,再从点Pn+1作直线平行于y轴,交曲线C于点Qn+1.Qn(n=1,2,3,…)的横坐标构成数列{an}.
设a>0,如图,已知直线l:y=ax及曲线C:y=x2,C上的点Q1的横坐标为a1(0<a1<a).从C上的点Qn(n≥1)作直线平行于x轴,交直线l于点Pn+1,再从点Pn+1作直线平行于y轴,交曲线C于点Qn+1.Qn(n=1,2,3,…)的横坐标构成数列{an}.