题目内容
已知直线l:y=ax+1-a(a∈R),若存在实数a使得一条曲线与直线l有两个不同的交点,且以这两个交点为端点的线段的长度恰好等于|a|,则称此曲线为直线l的“绝对曲线”.下面给出的三条曲线方程:
①y=-2|x-1|;
②(x-1)2+(y-1)2=1;
③x2+3y2=4.
其中直线l的“绝对曲线”有 .(填写全部正确选项的序号)
①y=-2|x-1|;
②(x-1)2+(y-1)2=1;
③x2+3y2=4.
其中直线l的“绝对曲线”有
分析:题目给出的是新定义题,给出的直线过定点(1,1),对于曲线y=-2|x-1|,通过分析其图象可知,直线l与该曲线不可能相交于两点,不符合新定义;对于曲线②(x-1)2+(y-1)2=1,直线l过该圆的圆心,所以a=±2时满足新定义;对于
曲线x2+3y2=4,假设该曲线是直线l的“绝对曲线”,把直线和其联立后看满足弦长等于a的值是否存在,由弦长公式得到关于a的方程,方程是高次方程,可以不求解,看方程对应函数的零点是否存在即可,利用根的存在性定理加以判断.
曲线x2+3y2=4,假设该曲线是直线l的“绝对曲线”,把直线和其联立后看满足弦长等于a的值是否存在,由弦长公式得到关于a的方程,方程是高次方程,可以不求解,看方程对应函数的零点是否存在即可,利用根的存在性定理加以判断.
解答:解:由y=ax+1-a=a(x-1)+1,可知直线l过点A(1,1).
对于①,y=-2|x-1|=
,图象是顶点为(1,0)的倒V型,而直线l过顶点A(1,1).
所以直线l不会与曲线y=-2|x-1|有两个交点,不是直线l的“绝对曲线”;
对于②,(x-1)2+(y-1)2=1是以A为圆心,半径为1的圆,
所以直线l与圆总有两个交点,且距离为直径2,所以存在a=±2,使得圆(x-1)2+(y-1)2=1与直线l有两个不同的交点,且以这两个交点为端点的线段的长度恰好等于|a|.
所以圆(x-1)2+(y-1)2=1是直线l的“绝对曲线”;
对于③,将y=ax+1-a代入x2+3y2=4,
得(3a2+1)x2+6a(1-a)x+3(1-a)2-4=0.
x1+x2=
,x1x2=
.
若直线l被椭圆截得的线段长度是|a|,
则a2=(x1-x2)2+(y1-y2)2=(x1-x2)2+(ax1+1-a-ax2-1+a)2
=(a2+1)[(x1+x2)2-4x1x2]
=(a2+1)[
-4
].
化简得
=(
)2.
令f(a)=
-(
)2.
f(1)=
-22=-
<0,f(3)=
-(
)2=
>0.
所以函数f(a)在(1,3)上存在零点,即方程
=(
)2有根.
而直线过椭圆上的定点(1,1),当a∈(1,3)时满足直线与椭圆相交.
故曲线x2+3y2=4是直线的“绝对曲线”.
故答案为②③.
对于①,y=-2|x-1|=
|
所以直线l不会与曲线y=-2|x-1|有两个交点,不是直线l的“绝对曲线”;
对于②,(x-1)2+(y-1)2=1是以A为圆心,半径为1的圆,
所以直线l与圆总有两个交点,且距离为直径2,所以存在a=±2,使得圆(x-1)2+(y-1)2=1与直线l有两个不同的交点,且以这两个交点为端点的线段的长度恰好等于|a|.
所以圆(x-1)2+(y-1)2=1是直线l的“绝对曲线”;
对于③,将y=ax+1-a代入x2+3y2=4,
得(3a2+1)x2+6a(1-a)x+3(1-a)2-4=0.
x1+x2=
| 6a(1-a) |
| 3a2+1 |
| 3(1-a)2-4 |
| 3a2+1 |
若直线l被椭圆截得的线段长度是|a|,
则a2=(x1-x2)2+(y1-y2)2=(x1-x2)2+(ax1+1-a-ax2-1+a)2
=(a2+1)[(x1+x2)2-4x1x2]
=(a2+1)[
| 36a2(1-a)2 |
| (3a2+1)2 |
| 3(1-a)2-4 |
| 3a2+1 |
化简得
| a2 |
| a2+1 |
| 6a+2 |
| 3a2+1 |
令f(a)=
| a2 |
| a2+1 |
| 6a+2 |
| 3a2+1 |
f(1)=
| 1 |
| 2 |
| 7 |
| 2 |
| 9 |
| 10 |
| 5 |
| 7 |
| 191 |
| 490 |
所以函数f(a)在(1,3)上存在零点,即方程
| a2 |
| a2+1 |
| 6a+2 |
| 3a2+1 |
而直线过椭圆上的定点(1,1),当a∈(1,3)时满足直线与椭圆相交.
故曲线x2+3y2=4是直线的“绝对曲线”.
故答案为②③.
点评:本题考查了两点间的距离公式,考查了直线与圆锥曲线的关系,考查了数学转化思想方法及运算能力,特别是对③的判断,能够考查学生灵活处理问题的能力,是有一定难度题目.

练习册系列答案
相关题目
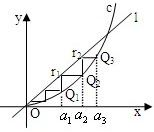 设a>0,如图,已知直线l:y=ax及曲线C:y=x2,C上的点Q1的横坐标为a1(0<a1<a).从C上的点Qn(n≥1)作直线平行于x轴,交直线l于点Pn+1,再从点Pn+1作直线平行于y轴,交曲线C于点Qn+1.Qn(n=1,2,3,…)的横坐标构成数列{an}.
设a>0,如图,已知直线l:y=ax及曲线C:y=x2,C上的点Q1的横坐标为a1(0<a1<a).从C上的点Qn(n≥1)作直线平行于x轴,交直线l于点Pn+1,再从点Pn+1作直线平行于y轴,交曲线C于点Qn+1.Qn(n=1,2,3,…)的横坐标构成数列{an}.