��Ŀ����
18��ij��ҵ����A��B���ֲ�Ʒ������ÿһ�ֲ�Ʒ������Ͷ�����ú��������±���| �� Ʒ Ʒ �� | �� �� �� | ú���֣� | �磨ǧ�ߣ� |
| A �� Ʒ | 3 | 9 | 4 |
| B �� Ʒ | 10 | 4 | 5 |
���� ������֪�����г�Լ����������Ŀ�꺯���������Թ滮����������
���  �⣺������A��B���ֲ�Ʒ�ֱ�Ϊx��y�֣�����Ϊz��Ԫ��
�⣺������A��B���ֲ�Ʒ�ֱ�Ϊx��y�֣�����Ϊz��Ԫ��
������ɵã�$\left\{\begin{array}{l}{3x+10y��300}\\{9x+4y��360}\\{4x+5y��200}\\{x��0��y��0}\end{array}\right.$��Ŀ�꺯��Ϊz=7x+12y��
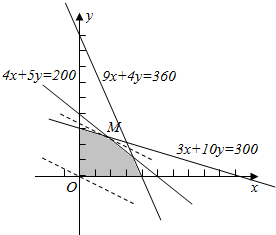
������������ͼ��6-2��Ӱ������ʾ��
��ֱ��7x+12y=0����ƽ�ƣ�����M��20��24��ʱzȡ�����ֵ��
���Ը���ҵ����A��B���ֲ�Ʒ�ֱ�Ϊ20����24��ʱ���������
���� ���⿼�����Թ滮�ļ�Ӧ�ã��г�Լ�����������������ǽ���Ĺؼ���������˼ά���������������

��ϰ��ϵ�д�
�����Ŀ
13�������ĸ���������������ǣ�������
| A�� | ��������p��x0��y0����ֱ�߶������÷���y-y0=k��x-x0����ʾ | |
| B�� | ��������������ͬ�ĵ�p1��x1��y1����p2��x2��y2����ֱ�߶������÷��̣�y-y1����x2-x1��=��x-x1����y2-y1����ʾ | |
| C�� | ��������A��0��b����ֱ�߶������÷���y=kx+b��ʾ | |
| D�� | ������ԭ���ֱ�߶������÷���$\frac{x}{a}$+$\frac{y}{b}$=1��ʾ |
10��������x2-1+��x2+3x+2��i�Ǵ���������ʵ��x��ֵ�ǣ�������
| A�� | 1 | B�� | 1��-1 | C�� | -1 | D�� | -2 |
8���ڡ�ABC�У���2bccosBcosC=b2sin2C+c2sin2B����ô��ABC�ǣ�������
| A�� | ���������� | B�� | �ȱ������� | C�� | ֱ�������� | D�� | ����ֱ�������� |