题目内容
(2012•贵州模拟)已知
,目标函数z=x-y的最大值为a,最小值为b,则(at+b)6展开式中t4的系数为( )
|
分析:通过线性规划,利用最值求出a与b的值,然后通过二项式定理求出(at+b)6展开式中t4的系数即可.
解答: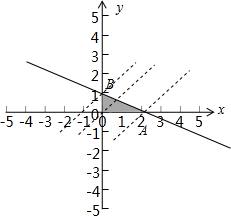 解:约束条件
解:约束条件
表示的可行域如图:目标函数z=x-y经过A,B两点分别取得最大值和最小值,A(2,0),B(0,1),所以
a=2,b=-1,
则(at+b)6展开式中t4的系数,就是(2t-1)6展开式中t4的系数.
即:
24 (-1)4=240.
故选B.
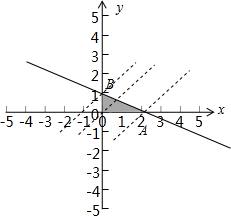 解:约束条件
解:约束条件
|
a=2,b=-1,
则(at+b)6展开式中t4的系数,就是(2t-1)6展开式中t4的系数.
即:
| C | 2 6 |
故选B.
点评:本题考查线性规划以及二项式定理的应用,考查计算能力.

练习册系列答案
相关题目