题目内容
在平面直角坐标系xoy两轴正方向有两点A (a, 0)、B(0, b)(a>2, b>2), 线段AB和圆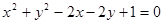 相切, 则△AOB的面积最小值为_____________.
相切, 则△AOB的面积最小值为_____________.
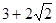
解析试题分析:根据题意,由于y两轴正方向有两点A (a, 0)、B(0, b)(a>2, b>2), 线段AB和圆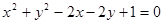 相切,那么圆心为(1,1),半径为1,那么直线AB为
相切,那么圆心为(1,1),半径为1,那么直线AB为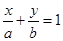 ,那么可知利用截距来表示边长结合相切时的等式关系可知,
,那么可知利用截距来表示边长结合相切时的等式关系可知,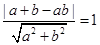 ,然后可知△AOB的面积最小值为
,然后可知△AOB的面积最小值为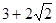 。
。
考点:直线与圆的位置关系
点评:解决的关键是利用直线与圆相切可知圆心到直线的距离等于半径,结合三角形的面积公式得到,属于基础题。

练习册系列答案
相关题目
 经过圆
经过圆 的圆心,则抛物线E的准线与圆F相交所得的弦长为 .
的圆心,则抛物线E的准线与圆F相交所得的弦长为 . ,AB=3,则切线AD的长为___ _____.
,AB=3,则切线AD的长为___ _____.
 轴上,且过两点
轴上,且过两点 的圆的方程为 .
的圆的方程为 .  ,直线
,直线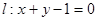 ,
, 的顶点A在直线
的顶点A在直线 上,顶点B、C都在圆M上,且边AB过圆心M,
上,顶点B、C都在圆M上,且边AB过圆心M, .则点A横坐标的最大值是 ;
.则点A横坐标的最大值是 ; (
( 是实数)与圆
是实数)与圆 相交于
相交于 两点,且
两点,且 (
( 是坐标原点)是直角三角形,则点
是坐标原点)是直角三角形,则点 与点
与点 之间距离的最小值是 .
之间距离的最小值是 . 的点数共有______ 个。
的点数共有______ 个。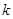 为何实数,直线
为何实数,直线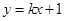 与曲线
与曲线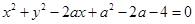 恒有交点,则实数
恒有交点,则实数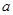 的取值范围为 。
的取值范围为 。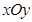 中,“直线
中,“直线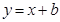 ,
,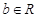 与曲线
与曲线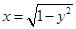 相切”的充要条件是 .
相切”的充要条件是 .