题目内容
18.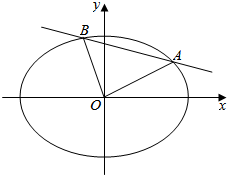 已知A,B为椭圆$C:\frac{x^2}{2}+{y^2}=1$上两个不同的点,O为坐标原点.设直线OA,OB,AB的斜率分别为k1,k2,k.
已知A,B为椭圆$C:\frac{x^2}{2}+{y^2}=1$上两个不同的点,O为坐标原点.设直线OA,OB,AB的斜率分别为k1,k2,k.(Ⅰ) 当k1=2时,求|OA|;
(Ⅱ) 当k1k2-1=k1+k2时,求k的取值范围.
分析 (Ⅰ)由直线OA斜率k1=2,得直线OA的方程为y=2x,代入椭圆方程得出交点,再利用两点之间的距离公式即可得出.
(Ⅱ) 设点A(x1,y1),B(x2,y2),直线AB的方程为y=kx+b.与椭圆方程联立可得(1+2k2)x2+4kbx+2b2-2=0,△>0,再利用根与系数的关系、斜率计算公式即可得出.
解答 解:(Ⅰ)由直线OA斜率k1=2,得直线OA的方程为y=2x,
代入椭圆方程得${x^2}=\frac{2}{9}$,
∴$|{OA}|=\sqrt{{x^2}+{{(2x)}^2}}=\frac{{\sqrt{10}}}{3}$.
(Ⅱ) 设点A(x1,y1),B(x2,y2),直线AB的方程为y=kx+b.
由$\left\{\begin{array}{l}\frac{x^2}{2}+{y^2}=1\\ y=kx+b\end{array}\right.$消去y得(1+2k2)x2+4kbx+2b2-2=0,
故△=16k2-8b2+8>0,且$\left\{\begin{array}{l}{x_1}+{x_2}=-\frac{4kb}{{2{k^2}+1}}\\{x_1}{x_2}=\frac{{2{b^2}-2}}{{2{k^2}+1}}.\end{array}\right.$①,
由k1+k2=k1k2-1得x2y1+x1y2=y1y2-x1x2,
将y1=kx1+b,y2=kx2+b代入得$({k^2}-2k-1){x_1}{x_2}+b(k-1)({x_1}+{x_2})+{b^2}=0$,②
将①代入②得b2=-2k2+4k+2,
联立△>0与b2≥0得$\left\{\begin{array}{l}4{k^2}-4k-1>0\\-2{k^2}+4k+2≥0\end{array}\right.$,
解得k的取值范围为$[{1-\sqrt{2},\frac{{1-\sqrt{2}}}{2}})∪({\frac{{1+\sqrt{2}}}{2},1+\sqrt{2}}]$.
点评 本题主要考查椭圆的几何性质、直线与椭圆的位置关系等基础知识,同时考查解析几何的基本思想方法和综合解题能力,属于难题.

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案| A. | 若m∥α,n∥α则m∥n | B. | 若m?α,m∥n,则n∥α | C. | 若m⊥α,α⊥β,则m∥β | D. | 若m⊥α,n∥α,则m⊥n |
| A. | f(x2)<f(x-1) | B. | (x-1)f(x)<xf(x+1) | C. | f(x)>x-1 | D. | f(x)<0 |
| A. | $\sqrt{2}$+1 | B. | 2$\sqrt{2}$+1 | C. | $\sqrt{5+2\sqrt{2}}$ | D. | $\sqrt{5-2\sqrt{2}}$ |
| A. | $[\frac{ln3}{3},\frac{1}{e})$ | B. | $[\frac{4ln3}{3},\frac{4}{e})$ | C. | $(0,\frac{1}{e})$ | D. | $(0,\frac{4}{e})$ |
| A. | $\frac{1}{6}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |