题目内容
4.已知命题p:方程x2-mx+1=0有实数解,命题q:x2-2x+m>0对任意x恒成立,若命题q∨(p∧q)为真,¬p为真,则实数m的取值范围是1<m<2.分析 分别求出关于p,q的不等式的m的范围,结合命题q∨(p∧q)为真,¬p为真,得到p假q真,从而求出m的范围.
解答 解:对于命题p:方程x2-mx+1=0有实数解,
则△=m2-4≥0,解得:m≥2或m≤-2,
命题q:x2-2x+m>0对任意x恒成立,
则△=4-4m<0,解得:m>1,
若命题q∨(p∧q)为真,¬p为真,
则p假q真,
则实数m的取值范围是:1<m<2
故答案为:1<m<2.
点评 本题考查了复合命题的判断,考查不等式的解法,是一道基础题.

练习册系列答案
相关题目
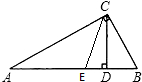 如图,Rt△ABC被斜边上的高CD和直角平分线CE分成3个三角形,S△ACE=30,S△CED=6,则△BCD的面积为( )
如图,Rt△ABC被斜边上的高CD和直角平分线CE分成3个三角形,S△ACE=30,S△CED=6,则△BCD的面积为( )