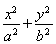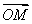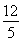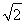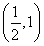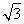题目内容
如图所示,已知直线l:y=x,圆C1的圆心为(3,0),且经过点A(4,1).
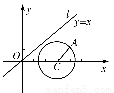
(1)求圆C1的方程;
(2)若圆C2与圆C1关于直线l对称,点B、D分别为圆C1、C2上任意一点,求|BD|的最小值.
(1)(x-3)2+y2=2.(2)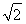
【解析】(1)依题意,设圆C1的方程为(x-3)2+y2=r2,因为圆C1经过点A(4,1),所以r2=(4-3)2+12=2.所以圆C1的方程为(x-3)2+y2=2.
(2)由(1),知圆C1的圆心坐标为(3,0),半径为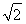 ,
,
C1到直线l的距离d=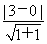 =
=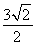 ,
,
所以圆C1上的点到直线l的最短距离为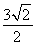 -
-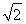 =
=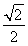 .
.
因为圆C2与圆C1关于直线l对称,所以|BD|min=2×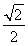 =
=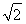

练习册系列答案
相关题目