题目内容
(本小题共12分)
如图,已知直线l与抛物线 相切于点P(2,1),且与x轴交于点A,O为坐标原点,
相切于点P(2,1),且与x轴交于点A,O为坐标原点,
定点B的坐标为(2,0).

(1)若动点M满足 ,求点M的轨迹C;
,求点M的轨迹C;
(2)若过点B的直线l′(斜率不等于零)与(I)中的轨迹C交于不同的两点E、F(E在B、F之间),试求△OBE与△OBF面积之比的取值范围.
【答案】
(I)动点M的轨迹C为以原点为中心,焦点在x轴上,长轴长为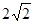 ,短轴长为2的椭圆
(II)(3-2
,短轴长为2的椭圆
(II)(3-2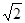 ,1).
,1).
【解析】
试题分析:(I)由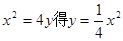 ,
, 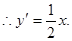 ∴直线l的斜率为
∴直线l的斜率为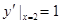
故l的方程为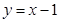 ,∴点A坐标为(1,0)
,∴点A坐标为(1,0)
设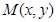 则
则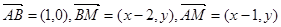 ,
,
由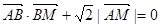 得
得 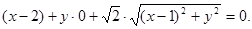
整理,得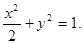
∴动点M的轨迹C为以原点为中心,焦点在x轴上,长轴长为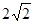 ,短轴长为2的椭圆
,短轴长为2的椭圆
(II)由题意知直线l的斜率存在且不为零,设l方程为y=k(x-2)(k≠0)①
将①代入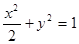 ,整理,得
,整理,得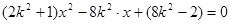 ,
,
由△>0得0<k2<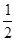 . 设E(x1,y1),F(x2,y2)
. 设E(x1,y1),F(x2,y2)
则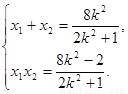 ②
②
令 ,由此可得
,由此可得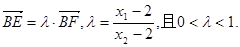
由②知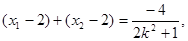
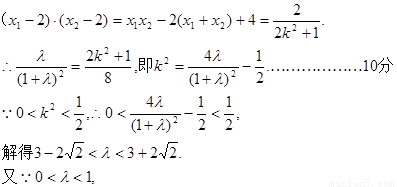
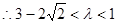 .
.
∴△OBE与△OBF面积之比的取值范围是(3-2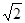 ,1).
,1).
考点:本题考查了直线与抛物线的位置关系
点评:对于直线与圆锥曲线的综合问题,往往要联立方程,同时结合一元二次方程根与系数的关系进行求解;而对于最值问题,则可将该表达式用直线斜率k表示,然后根据题意将其进行化简结合表达式的形式选取最值的计算方式.

练习册系列答案
相关题目
 ⊥平面
⊥平面 ,
, ∥
∥ 是正三角形,
是正三角形, ,且
,且 是
是 的中点
的中点
 ∥平面
∥平面 ;
; .
. 名,女同学有
名,女同学有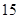 名,老师按照分层抽样的方法组建了一个
名,老师按照分层抽样的方法组建了一个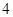 人的课外兴趣小组.
人的课外兴趣小组. 名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;


 ,
, ,求证:
,求证: .
. 的值.
的值.