题目内容
【题目】设函数![]() ,
,![]() ,其中
,其中![]() .
.
(1)若![]() ,
,![]() ,求函数在
,求函数在![]() 处的切线方程;
处的切线方程;
(2)讨论![]() 的单调区间.
的单调区间.
【答案】(1)![]() ;(2)a>0时,f(x)的增区间为(﹣∞,
;(2)a>0时,f(x)的增区间为(﹣∞,![]() ),(
),(![]() ,+∞),减区间为(
,+∞),减区间为(![]() ,
,![]() );a≤0时,f(x)的单调递增区间为(﹣∞,+∞),无减区间.
);a≤0时,f(x)的单调递增区间为(﹣∞,+∞),无减区间.
【解析】
(1)当a=1,b=2时,可得f(x),f′(x),而切线斜率k=f′(1),易求f(1),从而可得切点坐标,由点斜式可得切线方程;
(2)求出f(x)的导数,讨论a≤0时f′(x)≥0,f(x)在R上递增;当a>0时,由导数大于0,可得增区间;导数小于0,可得减区间;
(1)当a=1,b=2时,f(x)=x3﹣x-2,f′(x)=3x2﹣1,
则切线斜率k=f′(1)=2,
f(1)=1﹣1-2=-2,则切点为(1,-2),
∴函数f(x)在(1,f(1))处的切线方程为y+2=2(x﹣1),即y=2x-4;
(2)若f(x)=x3﹣ax﹣b,则f′(x)=3x2﹣a,
分两种情况讨论:
①当a≤0时,有f′(x)=3x2﹣a≥0恒成立,
此时f(x)的单调递增区间为(﹣∞,+∞),无减区间.
②当a>0时,令f′(x)=3x2﹣a=0,解得x![]() 或x
或x![]() ,
,
当x![]() 或x
或x![]() 时,f′(x)=3x2﹣a>0,f(x)为增函数,
时,f′(x)=3x2﹣a>0,f(x)为增函数,
当![]() x
x![]() 时,f′(x)=3x2﹣a<0,f(x)为减函数,
时,f′(x)=3x2﹣a<0,f(x)为减函数,
故f(x)的增区间为(﹣∞,![]() ),(
),(![]() ,+∞),减区间为(
,+∞),减区间为(![]() ,
,![]() );
);

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案【题目】大连市某企业为确定下一年投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:
(单位:![]() )和年利润
)和年利润![]() (单位:千元)的影响,对近8年的年宣传费
(单位:千元)的影响,对近8年的年宣传费![]() 和年销售量
和年销售量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.

|
|
|
|
|
|
|
46.6 | 573 | 6.8 | 289.8 | 1.6 | 215083.4 | 31280 |
表中![]() ,
,![]() .
.
根据散点图判断,
![]() 与
与![]() 哪一个适宜作为年销售量
哪一个适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
![]() 根据
根据![]() 的判断结果及表中数据,建立
的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
![]() 已知这种产品的年利润
已知这种产品的年利润![]() 与
与![]() 、
、![]() 的关系为
的关系为![]() .根据
.根据![]() 的结果回答下列问题:
的结果回答下列问题:
![]() 年宣传费
年宣传费![]() 时,年销售量及年利润的预报值是多少?
时,年销售量及年利润的预报值是多少?
![]() 年宣传费
年宣传费![]() 为何值时,年利润的预报值最大?
为何值时,年利润的预报值最大?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
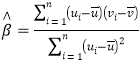 ,
,![]() .
.
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg),其频率分布直方图如下:

(1)根据箱产量的频率分布直方图填写下面![]() 列联表,从等高条形图中判断箱产量是否与新、旧网箱养殖方法有关;
列联表,从等高条形图中判断箱产量是否与新、旧网箱养殖方法有关;
(2)根据列联表判断是否有99%的把握认为箱产量与养殖方法有关?
箱产量<50kg | 箱产量≥50kg | |
旧养殖法 | ||
新养殖法 |
参考公式:
(1)给定临界值表
P(K | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)![]() 其中
其中![]() 为样本容量.
为样本容量.
