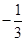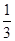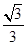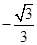题目内容
在△ABC中,角A,B,C所对的边分别是a,b,c,设平面向量e1=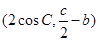 ,e2=
,e2=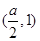 ,且e1⊥e2.
,且e1⊥e2.
(1)求cos 2A的值;
(2)若a=2,求△ABC的周长L的取值范围.
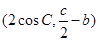 ,e2=
,e2=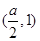 ,且e1⊥e2.
,且e1⊥e2.(1)求cos 2A的值;
(2)若a=2,求△ABC的周长L的取值范围.
(1)-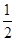 (2)(4,6]
(2)(4,6]
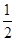 (2)(4,6]
(2)(4,6](1)∵e1⊥e2,∴e1·e2=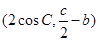 ·
·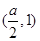 =2cos C·
=2cos C·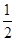 a+
a+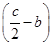 ·1=0,
·1=0,
即acos C+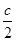 -b=0∴2acos C+c-2b=0.
-b=0∴2acos C+c-2b=0.
根据正弦定理得:2sin Acos C+sin C=2sin B,
∴2sin Acos C+sin C=2sin(A+C),
∴2sin Acos C+sin C=2sin Acos C+2cos Asin C,
∴2cos Asin C=sin C,∵sin C≠0,
∴cos A=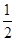 ,A∈(0,π)∴A=
,A∈(0,π)∴A=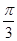 ∴cos 2A=cos
∴cos 2A=cos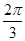 =-
=-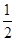 .
.
(2)由余弦定理得
a2=b2+c2-2bccos A=b2+c2-bc=(b+c)2-3bc≥(b+c)2-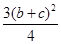 =
=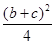 即b+c≤
即b+c≤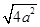 =4,当且仅当b=c=2时取等号,由构成三角形的条件知b+c>a=2,即b+c∈(2,4]∴L=a+b+c∈(4,6].
=4,当且仅当b=c=2时取等号,由构成三角形的条件知b+c>a=2,即b+c∈(2,4]∴L=a+b+c∈(4,6].
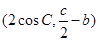 ·
·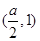 =2cos C·
=2cos C·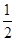 a+
a+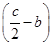 ·1=0,
·1=0,即acos C+
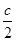 -b=0∴2acos C+c-2b=0.
-b=0∴2acos C+c-2b=0.根据正弦定理得:2sin Acos C+sin C=2sin B,
∴2sin Acos C+sin C=2sin(A+C),
∴2sin Acos C+sin C=2sin Acos C+2cos Asin C,
∴2cos Asin C=sin C,∵sin C≠0,
∴cos A=
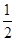 ,A∈(0,π)∴A=
,A∈(0,π)∴A=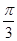 ∴cos 2A=cos
∴cos 2A=cos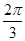 =-
=-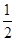 .
.(2)由余弦定理得
a2=b2+c2-2bccos A=b2+c2-bc=(b+c)2-3bc≥(b+c)2-
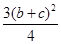 =
=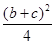 即b+c≤
即b+c≤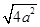 =4,当且仅当b=c=2时取等号,由构成三角形的条件知b+c>a=2,即b+c∈(2,4]∴L=a+b+c∈(4,6].
=4,当且仅当b=c=2时取等号,由构成三角形的条件知b+c>a=2,即b+c∈(2,4]∴L=a+b+c∈(4,6].
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
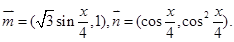 记
记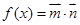 .
.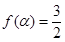 ,求
,求 的值;
的值; 、
、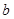 、
、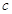 ,且满足
,且满足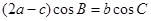 ,若
,若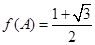 ,试判断△ABC的形状.
,试判断△ABC的形状.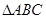 中,角
中,角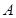 、
、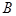 、
、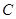 的对边分别为
的对边分别为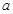 、
、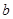 、
、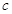 .设向量
.设向量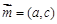 ,
,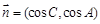 .
.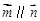 ,
,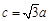 ,求角
,求角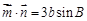 ,
,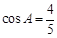 ,求
,求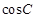 的值.
的值. 中,a,b,c分别为内角A,B,C的对边,已知:
中,a,b,c分别为内角A,B,C的对边,已知: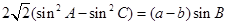 ,
, .
.
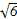 +
+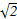 )海里/小时
)海里/小时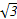 )海里/小时
)海里/小时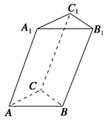
 ABC中,若
ABC中,若 、
、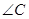 的对边长分别为b、c,
的对边长分别为b、c,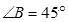 ,
,
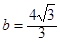 ,则
,则 ( )
( )
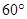

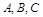 所对应的边分别为
所对应的边分别为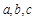 ,若a=9,b=6, A=
,若a=9,b=6, A=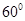 ,则
,则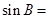 ( )
( )