题目内容
不等式选讲.
设函数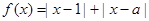 .
.
(1)若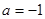 解不等式
解不等式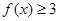 ;
;
(2)如果关于 的不等式
的不等式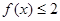 有解,求
有解,求 的取值范围.
的取值范围.
(Ⅰ)原不等式的解为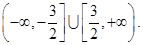
(Ⅱ) 的取值范围为
的取值范围为
解析试题分析:(Ⅰ)当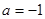 时,
时,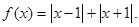
由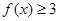 ,得,
,得,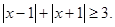
①当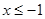 时,不等式化为
时,不等式化为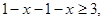 即
即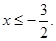
所以,原不等式的解为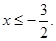
②当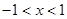 时,不等式化为
时,不等式化为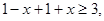 即
即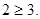
所以,原不等式无解.
③ 当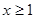 时,不等式化为
时,不等式化为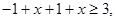 即
即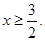
所以,原不等式的解为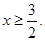
综上,原不等式的解为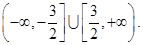 5分
5分
(说明:若考生按其它解法解答正确,相应给分)
(Ⅱ)因为关于 的不等式
的不等式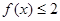 有解,所以,
有解,所以,
因为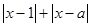 表示数轴上的点到
表示数轴上的点到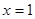 与
与 两点的距离之和,
两点的距离之和,
所以,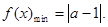
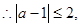 解得,
解得,
所以, 的取值范围为
的取值范围为 10分
10分
考点:绝对值不等式的解法
点评:中档题,绝对值不等式的解法,往往从“去”绝对值的符号入手,主要方法有“平方法”“分类讨论法”,有时利用绝对值的几何意义,会简化解题过程。

练习册系列答案
相关题目
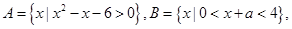 若
若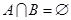 ,求实数
,求实数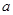 的取值范围;
的取值范围;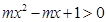 ,对任意实数
,对任意实数 都成立,求
都成立,求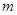 的取值范围.
的取值范围.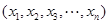 满足条件:
满足条件: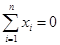 ; ②
; ②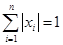 .
.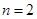 时,求
时,求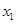 ,
,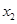 的值;
的值;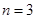 时,求证:
时,求证: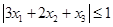 ;
;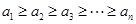 ,且
,且
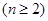 ,求证:
,求证: .
.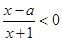 的解集为P,不等式
的解集为P,不等式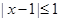 的解集为Q.
的解集为Q.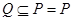 求正数a的取值范围
求正数a的取值范围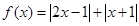 .
.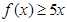 ;
;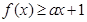 的解集为
的解集为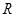 ,求实数
,求实数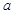 的取值范围.
的取值范围.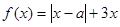 ,其中
,其中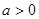 .
.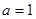 时,求不等式
时,求不等式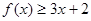 的解集;
的解集; 的解集为
的解集为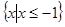 ,求
,求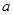 的值.
的值.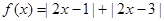 ,
,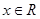 .
. ;
;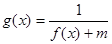 的定义域为
的定义域为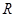 ,求实数
,求实数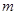 的取值范围.
的取值范围.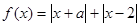
 的解集
的解集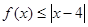 的解集包含[1,2],求
的解集包含[1,2],求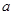 的取值范围
的取值范围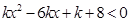 的解集为空集,求实数k的取值范围.
的解集为空集,求实数k的取值范围.