题目内容
已知 在[0,1]上是
在[0,1]上是 的减函数,则
的减函数,则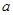 的取值范围是
的取值范围是
 在[0,1]上是
在[0,1]上是 的减函数,则
的减函数,则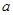 的取值范围是
的取值范围是 1<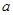 <2
<2
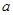 <2
<2【错解分析】∵
 是由
是由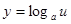 ,
, 复合而成,又
复合而成,又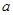 >0
>0∴
 在[0,1]上是
在[0,1]上是 的减函数,由复合函数关系知
的减函数,由复合函数关系知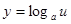 应为增函数,
应为增函数,∴
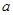 >1
>1【正解】∵
 是由
是由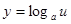 ,
, 复合而成,又
复合而成,又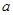 >0
>0∴
 在[0,1]上是
在[0,1]上是 的减函数,由复合函数关系知
的减函数,由复合函数关系知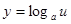 应为增函数,
应为增函数,∴
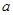 >1
>1又由于
 在[0,1]上时
在[0,1]上时  有意义,
有意义, 又是减函数,
又是减函数,∴
 =1时,
=1时, 取最小值是
取最小值是 >0即可,∴
>0即可,∴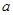 <2
<2综上可知所求的取值范围是1<
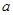 <2
<2【点评】解题中虽然考虑了对数函数与一次函数复合关系,却忽视了数定义域的限制,单调区间应是定义域的某个子区间,即函数应在[0,1]上有意义.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 ,则满足不等式
,则满足不等式 的x的范围是( )
的x的范围是( )

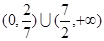

 是( )
是( ) 上单调递增
上单调递增 上单调递增
上单调递增 在
在 上为增函数,则实数a的取值范围为___________;
上为增函数,则实数a的取值范围为___________;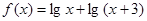 的定义域为 .
的定义域为 .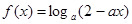 在
在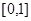 上为减函数,则
上为减函数,则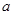 的取值范围为( )。
的取值范围为( )。


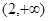
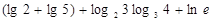 =_______
=_______ (2x+1)在(-
(2x+1)在(- ,0)内恒有f(x)>0,则a的取值范围是( )
,0)内恒有f(x)>0,则a的取值范围是( ) <a<-1或1<a<
<a<-1或1<a<