题目内容
设方程10x=|lg(-x)|的两个根分别为x1,x2,则
| A.x1 x2<0 | B.x1 x2=1 | C.Xi X2 >1 | D.0<x1 x2<1 |
D
试题分析:根据题意可知,方程10x=|lg(-x)|的两个根分别为
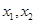 ,作图y=10x,和y=|lg(-x)|,结合图像可知,交点的坐标落在原点和(1,0)点之间,显然说明了两个根的取值范围是(0,1),故选D.
,作图y=10x,和y=|lg(-x)|,结合图像可知,交点的坐标落在原点和(1,0)点之间,显然说明了两个根的取值范围是(0,1),故选D.点评:解决该试题的关键是利用数形结合思想来分析图像与图像的交点位置,进而判定交点的横坐标的范围,从而得到结论。属于中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则这四个数的大小关系是( )
,则这四个数的大小关系是( )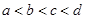

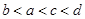

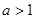 ,若仅有一个常数c使得对于任意的
,若仅有一个常数c使得对于任意的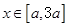 ,都有
,都有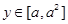 满足方程
满足方程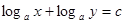 ,这时,实数
,这时,实数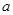 的取值的集合为 。
的取值的集合为 。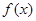 是定义在实数集R上的奇函数,且在区间
是定义在实数集R上的奇函数,且在区间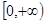 上是单调递增,若
上是单调递增,若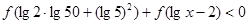 ,则
,则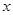 的取值范围为 .
的取值范围为 .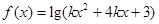 的定义域是R,则非零实数
的定义域是R,则非零实数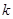 的取值范围是 。
的取值范围是 。 其中
其中 .
. 是
是 上的减函数;
上的减函数; ,求
,求 的取值范围.
的取值范围.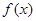 =
=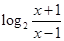 .
.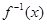 ,并求使得函数
,并求使得函数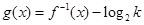 有零点的实数
有零点的实数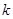 的取值范围.
的取值范围. 在[0,1]上是
在[0,1]上是 的减函数,则
的减函数,则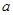 的取值范围是
的取值范围是 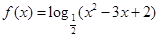 的单调递增区间是 .
的单调递增区间是 .