题目内容
(本小题12分)已知数列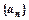 是等差数列,
是等差数列,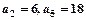 ;数列
;数列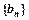 的前n项和是
的前n项和是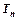 ,且
,且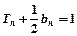 .
.
(Ⅰ)求数列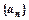 的通项公式;
的通项公式;
(II)求证:数列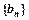 是等比数列;
是等比数列;
(Ⅲ)记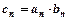 ,求
,求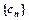 的前n项和
的前n项和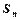 .
.
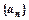 是等差数列,
是等差数列,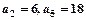 ;数列
;数列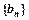 的前n项和是
的前n项和是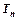 ,且
,且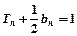 .
.(Ⅰ)求数列
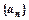 的通项公式;
的通项公式; (II)求证:数列
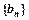 是等比数列;
是等比数列;(Ⅲ)记
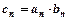 ,求
,求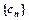 的前n项和
的前n项和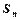 .
.(Ⅰ)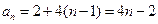
(II)略
(Ⅲ)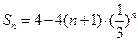
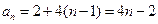
(II)略
(Ⅲ)
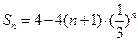
解:(Ⅰ)设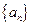 的公差为
的公差为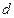 ,则:
,则: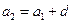 ,
,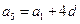 ,
,
∵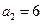 ,
,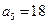 ,∴
,∴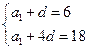 ,∴
,∴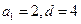 . ……………………2分
. ……………………2分
∴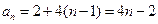 . ……………………4分
. ……………………4分
(II)当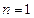 时,
时,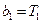 ,由
,由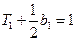 ,得
,得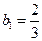 . ……………………5分
. ……………………5分
当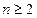 时,
时,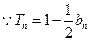 ,
, ,
,
∴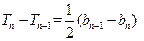 ,即
,即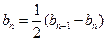 . …………………………7分
. …………………………7分
∴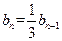 .
.
∴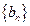 是以
是以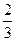 为首项,
为首项,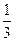 为公比的等比数列. ………………………8分
为公比的等比数列. ………………………8分
(Ⅲ)由(2)可知: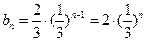 . ………………………9分
. ………………………9分
∴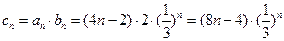 . …………………10分
. …………………10分
∴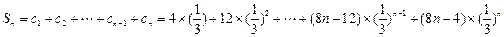 .
.
∴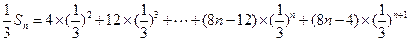 .
.
∴
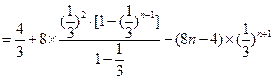
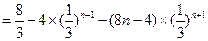 . …………………………13分
. …………………………13分
∴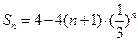 . …………………………14分
. …………………………14分
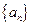 的公差为
的公差为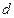 ,则:
,则: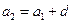 ,
,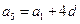 ,
,∵
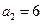 ,
,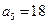 ,∴
,∴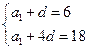 ,∴
,∴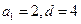 . ……………………2分
. ……………………2分∴
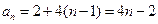 . ……………………4分
. ……………………4分(II)当
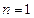 时,
时,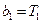 ,由
,由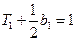 ,得
,得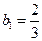 . ……………………5分
. ……………………5分当
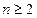 时,
时,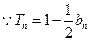 ,
, ,
,∴
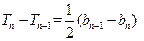 ,即
,即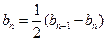 . …………………………7分
. …………………………7分∴
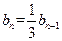 .
. ∴
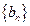 是以
是以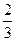 为首项,
为首项,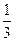 为公比的等比数列. ………………………8分
为公比的等比数列. ………………………8分(Ⅲ)由(2)可知:
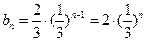 . ………………………9分
. ………………………9分∴
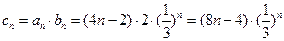 . …………………10分
. …………………10分∴
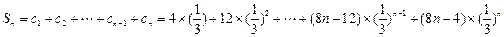 .
.∴
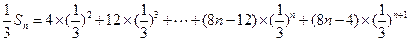 .
.∴

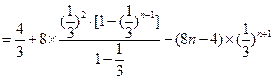
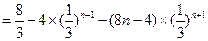 . …………………………13分
. …………………………13分∴
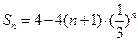 . …………………………14分
. …………………………14分
练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
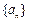 的前
的前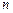 项和为
项和为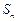 ,
,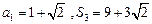
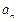 与前
与前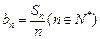 求证:数列
求证:数列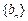 中任意不同的三项都不可能成为等比数列.
中任意不同的三项都不可能成为等比数列.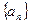 的各项均为正数,
的各项均为正数,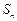 为其前
为其前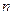 项和,对于任意
项和,对于任意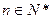 ,总有
,总有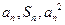 成等差数列.
成等差数列.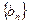 的前
的前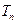 ,且
,且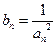 ,求证:对任意正整数
,求证:对任意正整数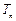
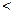 2;
2;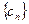 中,
中,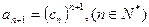 ,求数列
,求数列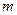 的三次幂可拆分成几个连续奇数的和,如右图所示,若
的三次幂可拆分成几个连续奇数的和,如右图所示,若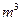 的“拆分数”中有一个数是2009,则
的“拆分数”中有一个数是2009,则
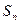 是等差数列
是等差数列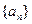 的前
的前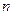 项和,
项和,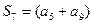 ,则
,则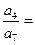 ( )
( ) 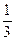
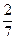
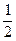
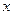 倍,则该工厂一年中的月平均增长率是( )
倍,则该工厂一年中的月平均增长率是( )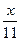

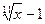
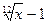
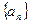 为等差数列,
为等差数列,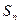 是其前项和,且
是其前项和,且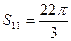 ,则
,则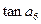 的值为( )
的值为( )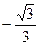

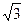
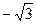
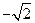 ,0,
,0,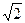 ……的第15项为 ( )
……的第15项为 ( )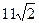

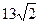
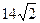
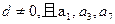 成等比数列,则
成等比数列,则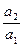 ="( " )
="( " )