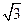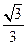题目内容
(本小题满分12分)
已知等差数列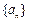 的前
的前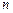 项和为
项和为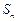 ,
,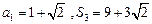
(1)求数列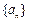 的通项公式
的通项公式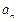 与前
与前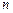 项和
项和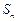 ;
;
(2)设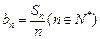 求证:数列
求证:数列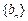 中任意不同的三项都不可能成为等比数列.
中任意不同的三项都不可能成为等比数列.
已知等差数列
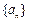 的前
的前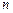 项和为
项和为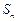 ,
,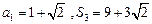
(1)求数列
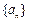 的通项公式
的通项公式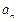 与前
与前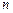 项和
项和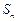 ;
;(2)设
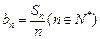 求证:数列
求证:数列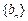 中任意不同的三项都不可能成为等比数列.
中任意不同的三项都不可能成为等比数列.(1)
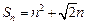 ,
,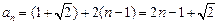
(2)略
解:(1)设数列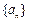 的差为
的差为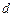 ,则
,则
所以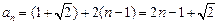
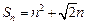
(2)由(1)知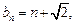 用反证法,假设数列
用反证法,假设数列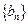 中存在三项
中存在三项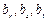
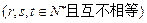 成等比数列,则
成等比数列,则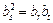 ,即
,即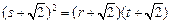
所以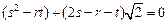 则
则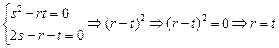
与r、s、t互不相等,矛盾,所以数列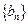 中任意三项都不可能成为等比数列
中任意三项都不可能成为等比数列
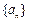 的差为
的差为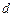 ,则
,则
所以
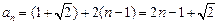
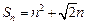
(2)由(1)知
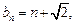 用反证法,假设数列
用反证法,假设数列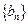 中存在三项
中存在三项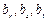
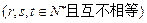 成等比数列,则
成等比数列,则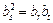 ,即
,即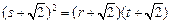
所以
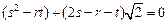 则
则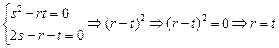
与r、s、t互不相等,矛盾,所以数列
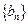 中任意三项都不可能成为等比数列
中任意三项都不可能成为等比数列
练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
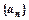 是等差数列,
是等差数列,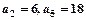 ;数列
;数列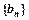 的前n项和是
的前n项和是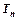 ,且
,且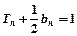 .
.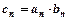 ,求
,求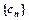 的前n项和
的前n项和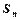 .
.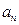 }的前5项和
}的前5项和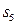 =25,且
=25,且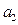 =3,则
=3,则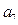 =
=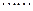 第6行的第二个数16=5+11,第三个数25=11+14
第6行的第二个数16=5+11,第三个数25=11+14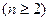 第2个数是 .
第2个数是 . 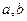 ,等比数列3,
,等比数列3,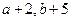 ,则该等差数列的公差为( )
,则该等差数列的公差为( )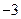
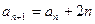 ,那么
,那么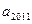 的值是( )
的值是( )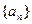 中,已知
中,已知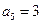 ,
,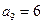 ,则
,则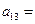 ( )
( )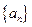 中,若
中,若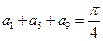 ,则
,则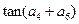 等于
等于