题目内容
【题目】已知函数f(x)=|xex|,方程f2(x)+tf(x)+1=0(t∈R)有四个实数根,则t的取值范围 .
【答案】![]()
【解析】解:f(x)=|xex|= 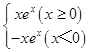 当x≥0时,f′(x)=ex+xex≥0恒成立,所以f(x)在[0,+∞)上为增函数;
当x≥0时,f′(x)=ex+xex≥0恒成立,所以f(x)在[0,+∞)上为增函数;
当x<0时,f′(x)=﹣ex﹣xex=﹣ex(x+1),
由f′(x)=0,得x=﹣1,当x∈(﹣∞,﹣1)时,f′(x)=﹣ex(x+1)>0,f(x)为增函数,
当x∈(﹣1,0)时,f′(x)=﹣ex(x+1)<0,f(x)为减函数,
所以函数f(x)=|xex|在(﹣∞,0)上有一个极大值为f(﹣1)=﹣(﹣1)e﹣1= ![]() ,
,
要使方程f2(x)+tf(x)+1=0(t∈R)有四个实数根,
令f(x)=m,则方程m2+tm+1=0应有两个不等根,且一个根在 ![]() 内,一个根在
内,一个根在 ![]() 内,
内,
再令g(m)=m2+tm+1,
因为g(0)=1>0,
则只需g( ![]() )<0,即
)<0,即 ![]() ,解得:t<﹣
,解得:t<﹣ ![]() .
.
所以,使得函数f(x)=|xex|,方程f2(x)+tf(x)+1=0(t∈R)有四个实数根的t的取值范围
是 ![]() .
.
所以答案是 ![]() .
.

练习册系列答案
相关题目