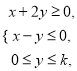题目内容
【题目】为了解某校学生的视力情况,现采用随机抽样的方法从该校的![]() 两班中各抽取
两班中各抽取![]() 名学生进行视力检测,检测的数据如下:
名学生进行视力检测,检测的数据如下:
![]() 班
班![]() 名学生的视力检测结果:
名学生的视力检测结果: ![]()
![]() 班
班![]() 名学生的视力检测结果:
名学生的视力检测结果: ![]()
(Ⅰ)分别计算两组数据的平均数,从计算结果看,哪个班的学生的视力较好?并计算![]() 班的
班的![]() 名学生视力的方差;
名学生视力的方差;
(Ⅱ)现从![]() 班的上述
班的上述![]() 名学生中随机选取
名学生中随机选取![]() 名,求这
名,求这![]() 名学生中至少有
名学生中至少有![]() 名学生的视力低于
名学生的视力低于![]() 的概率.
的概率.
【答案】(Ⅰ)详见解析; (Ⅱ) ![]() .
.
【解析】试题分析: (Ⅰ)分别计算出两个班的平均数进行比较,再利用方差公式计算![]() 班学生的数据;(Ⅱ)根据古典概型计算公式计算即可.
班学生的数据;(Ⅱ)根据古典概型计算公式计算即可.
试题解析:(Ⅰ) ![]() 班
班![]() 名学生的视力检测结果的平均数为
名学生的视力检测结果的平均数为
![]()
![]() 班
班![]() 名学生视力检测结果的平均数为
名学生视力检测结果的平均数为
![]()
从数据结果看![]() 班学生的视力较好
班学生的视力较好
![]() 班
班![]() 名学生视力的方差
名学生视力的方差
![]()
(Ⅱ)从![]() 班的
班的![]() 名学生中随机选取
名学生中随机选取![]() 名,则这
名,则这![]() 名学生视力检测结果有
名学生视力检测结果有
![]() 共
共![]() 个基本事件.其中这
个基本事件.其中这![]() 名学生中至少有
名学生中至少有![]() 名学生视力低于
名学生视力低于![]() 的基本事件有
的基本事件有![]() 个,所以所求的概率为
个,所以所求的概率为![]()
点睛:本题考查统计中平均数与方差的计算以及利用古典概型求概率,属于中档题目. 具有以下两个特点的概率模型称为古典概率模型,简称古典概型:(1)试验中所有可能出现的基本事件只有有限个.(2)每个基本事件出现的可能性相等.如果一次试验中可能出现的结果有n个,而且所有结果出现的可能性都相等,那么每一个基本事件的概率都是![]() ;如果某个事件A包括的结果有m个,那么事件A的概率P(A)=
;如果某个事件A包括的结果有m个,那么事件A的概率P(A)=![]() .
.

 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案【题目】下表是某校高三一次月考5个班级的数学、物理的平均成绩:
班级 | 1 | 2 | 3 | 4 | 5 |
数学( | 111 | 113 | 119 | 125 | 127 |
物理( | 92 | 93 | 96 | 99 | 100 |
(Ⅰ)一般来说,学生的物理成绩与数学成绩具有线性相关关系,根据上表提供的数据,求两个变量![]() ,
, ![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)从以上5个班级中任选两个参加某项活动,设选出的两个班级中数学平均分在115分以上的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:  ,
, ![]()