题目内容
某工厂计划生产A.B两种涂料,生产A种涂料1t需要甲种原料
1t.乙种原料2t,可获利润3千元;生产B种涂料1t需要甲种原料2t,乙种原料1t,
可获利润2千元,又知该工厂甲种原料的用量不超过400t,乙种原料的用量不超过500t,
问如何安排生产才能获得最大利润?(注:t表示重量单位“吨”)
1t.乙种原料2t,可获利润3千元;生产B种涂料1t需要甲种原料2t,乙种原料1t,
可获利润2千元,又知该工厂甲种原料的用量不超过400t,乙种原料的用量不超过500t,
问如何安排生产才能获得最大利润?(注:t表示重量单位“吨”)
应分别生产A、B两种涂料各200t、100t才能获得最大利润
本试题主要是考查了线性规划的最优解问题在实际生活中的运用。
根据已知设出变量设应分别生产A、B两种涂料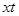 、
、 ,总利润为Z千元,那么得到x,y的关系式,以及总利润的表达式,进而结合平移法得到最值。
,总利润为Z千元,那么得到x,y的关系式,以及总利润的表达式,进而结合平移法得到最值。
解:设应分别生产A、B两种涂料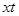 、
、 ,总利润为Z千元…………1分
,总利润为Z千元…………1分
则线性约束条件是:
目标函数 ………………6分
………………6分
作出可行域,如图所示
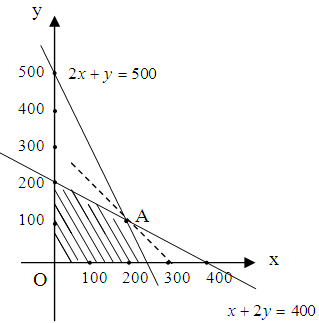 ………………8分
………………8分
平移可知,当直线
经过点A时,纵截距最大,则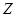 取得最大值。
取得最大值。
由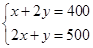 得
得  即A(200,100)
即A(200,100)
此时 千元 ………………11分
千元 ………………11分
答:应分别生产A、B两种涂料各200t、100t才能获得最大利润。…………12分
根据已知设出变量设应分别生产A、B两种涂料
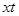 、
、 ,总利润为Z千元,那么得到x,y的关系式,以及总利润的表达式,进而结合平移法得到最值。
,总利润为Z千元,那么得到x,y的关系式,以及总利润的表达式,进而结合平移法得到最值。解:设应分别生产A、B两种涂料
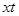 、
、 ,总利润为Z千元…………1分
,总利润为Z千元…………1分则线性约束条件是:

目标函数
 ………………6分
………………6分作出可行域,如图所示
 ………………8分
………………8分平移可知,当直线

经过点A时,纵截距最大,则
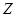 取得最大值。
取得最大值。由
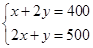 得
得  即A(200,100)
即A(200,100)此时
 千元 ………………11分
千元 ………………11分答:应分别生产A、B两种涂料各200t、100t才能获得最大利润。…………12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则z=3x+2y的最大值是 .
,则z=3x+2y的最大值是 . 满足约束条件
满足约束条件 (
( 为常数)时,能使
为常数)时,能使 的最大值为12
的最大值为12 满足线性约束条件
满足线性约束条件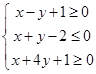 ,若
,若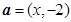 ,
,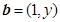 ,则
,则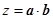 的最大值是( )
的最大值是( )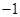
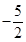
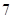
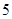
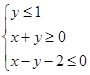 ,则
,则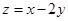 的最大值为( )
的最大值为( )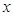 ,
,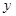 满足约束条件
满足约束条件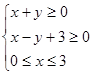 ,则
,则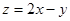 的最大值为( )
的最大值为( )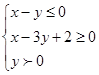 ,则(x-1)2+y2的取值范围是( )
,则(x-1)2+y2的取值范围是( )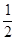 ,9)
,9)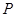 在直线
在直线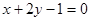 上,点
上,点 在直线
在直线 上,
上, 中点为
中点为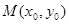 ,且
,且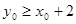 ,则
,则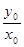 的取值范围为( ).
的取值范围为( ).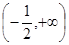
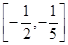
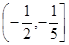
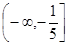
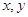 满足约束条件
满足约束条件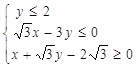 ,则目标函数
,则目标函数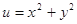 的最大值
的最大值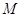 与最小值
与最小值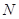 的比
的比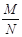 = ( )
= ( )